题目内容
已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
(1)当点C、E、F在直线AB的同侧时(如图1所示)
①若∠COF=28°,则∠BOE= °
②若∠COF=α°,则∠BOE= °.
(2)当点C与点E、F在直线AB的两旁(如图2所示)时,(1)中②是否仍然成立?请给出你的结论并说明理由.
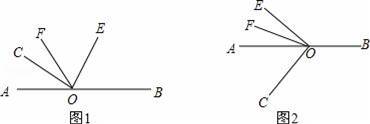

【考点】角的计算;角平分线的定义.
【分析】(1)①由余角的定义先求得∠FOE=62°,由角平分线的定义可求得∠AOE=124°,最后根据补角的定义可求得∠BOE的度数;
②由余角的定义先求得∠FOE=(90﹣α)°,由角平分线的定义可求得∠AOE=2∠EOF=180°﹣2α,最后根据补角的定义可求得∠BOE=2α;
(2)由余角的定义先求得∠FOE=(90﹣α)°,由角平分线的定义可求得∠AOE=2∠EOF=180°﹣2α,最后根据补角的定义可求得∠BOE=2α.
【解答】解:(1)①∵∠COE=90°,∠COF=28°,
∴∠EOF=90°﹣28°=62°.
∵OF是∠AOE的平分线,
∴∠AOE=2∠EOF=124°.
∴∠BOE=180°﹣∠AOE=180°﹣124°=56°.
②∵∠COE=90°,∠COF=α°,
∴∠EOF=90°﹣α°=(90﹣α)°.
∵OF是∠AOE的平分线,
∴∠AOE=2∠EOF=2×(90﹣α)=180°﹣2α.
∴∠BOE=180°﹣∠AOE=180°﹣=2α.
故答案为:①56°;②2α.
(2)成立.
理由:∵∠COE=90°,∠COF=α°,
∴∠EOF=90°﹣α°=(90﹣α)°.
∵OF是∠AOE的平分线,
∴∠AOE=2∠EOF=2×(90﹣α)=180°﹣2α.
∴∠BOE=180°﹣∠AOE=180°﹣=2α.
【点评】本题主要考查的是角的计算、补角和余角的定义,依据余角和邻补角的定义求得∠EOF和∠BOE的度数是解题的关键.

 备战中考寒假系列答案
备战中考寒假系列答案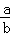 =﹣1;
=﹣1;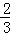 πxy的系数是
πxy的系数是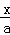 =
=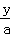 ,则x=y;
,则x=y;
 .
.
 的值为0,则x的值为( )
的值为0,则x的值为( ) 的结果是( )
的结果是( ) B.
B. C.
C. D.
D.