Question

【题目】⊙O的直径为2，AB，AC为⊙O的两条弦，AB=，AC=，则∠BAC=_____．

Answer 1

【答案】15°或75°．

【解析】

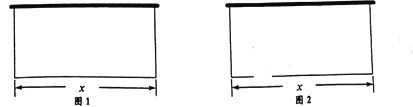
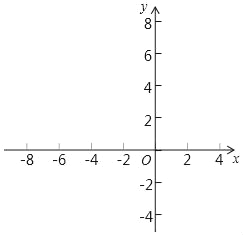
根据题意点C的位置有两种情况，如图1，∠BAC=∠CAO+∠OAB；如图2，∠BAC=∠OAB-∠OAC，进而得出答案．

解：如图1，连接OC，OA，OB，过点O作OE⊥AC于点E，

∵OA=OB=1，AB=，

12+12=（）2，

∴∠AOB=90°，

∴△OAB是等腰直角三角形，∠OAB=45°，

∵AC=，OE⊥AC，

∴AE= ，

∴cos∠EAO=，

∴∠EAO=30°，

∴如图1时，∠BAC=∠CAO+∠OAB=30°+45°=75°；

如图2时，∠BAC=∠BAC=∠OAB﹣∠OAC．=45°﹣30°=15°．

故答案为15°或75°．