题目内容
已知:如图,在平面直角坐标系 中,点
中,点 、点
、点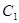 的坐标分别为
的坐标分别为 ,
, ,将△
,将△ 绕原点
绕原点 逆时针旋转
逆时针旋转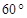 ,再将其各边都扩大为原来的
,再将其各边都扩大为原来的 倍,使
倍,使 ,得到△
,得到△ .将△
.将△ 绕原点
绕原点 逆时针旋转
逆时针旋转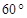 ,再将其各边都扩大为原来的
,再将其各边都扩大为原来的 倍,使
倍,使 ,得到△
,得到△ ,如此下去,得到△
,如此下去,得到△ .
.

(1) 的值是_______________;
的值是_______________;
(2)△ 中,点
中,点 的坐标:_____________.
的坐标:_____________.
 中,点
中,点 、点
、点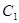 的坐标分别为
的坐标分别为 ,
, ,将△
,将△ 绕原点
绕原点 逆时针旋转
逆时针旋转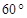 ,再将其各边都扩大为原来的
,再将其各边都扩大为原来的 倍,使
倍,使 ,得到△
,得到△ .将△
.将△ 绕原点
绕原点 逆时针旋转
逆时针旋转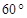 ,再将其各边都扩大为原来的
,再将其各边都扩大为原来的 倍,使
倍,使 ,得到△
,得到△ ,如此下去,得到△
,如此下去,得到△ .
.
(1)
 的值是_______________;
的值是_______________;(2)△
 中,点
中,点 的坐标:_____________.
的坐标:_____________.2;( ).
).
 ).
).考点:
专题:规律型.
分析:(1)易得OB =mOB
=mOB =OC
=OC ,根据最初的三角形中OB
,根据最初的三角形中OB ,OC
,OC 的关系可得m的值;
的关系可得m的值;
(2)可得旋转6次后,正好旋转一周,那么可得点C 的坐标跟C
的坐标跟C 的坐标在一条射线上,其横纵坐标均为原来的2010倍.
的坐标在一条射线上,其横纵坐标均为原来的2010倍.
解答:解:(1)在△OB C
C 中,
中,
∵OB =1,B
=1,B C
C =
= ,
,
∴tan∠C OB
OB =
= ,
,
∴∠C OB
OB =60°,OC
=60°,OC =2,
=2,
∵OB =mOB
=mOB ,OB
,OB =OC
=OC ,
,
∴m=2,
故答案为2;
(2)∵每一次的旋转角是60°,
∴旋转6次后C在x轴正半轴上,
∴2011÷6=335…1,
∴点C 的坐标跟C
的坐标跟C 的坐标在一条射线上,
的坐标在一条射线上,
∵第2次旋转后,各边长是原来的2倍,第3次旋转后,各边长是原来的22倍,
∴点C 的横纵坐标均为原来的2010倍.
的横纵坐标均为原来的2010倍.
故答案为( ).
).
点评:考查规律旋转后点的坐标;得到所求点的位置是解决本题的突破点;得到坐标的规律是解决本题的难点
专题:规律型.
分析:(1)易得OB
 =mOB
=mOB =OC
=OC ,根据最初的三角形中OB
,根据最初的三角形中OB ,OC
,OC 的关系可得m的值;
的关系可得m的值;(2)可得旋转6次后,正好旋转一周,那么可得点C
 的坐标跟C
的坐标跟C 的坐标在一条射线上,其横纵坐标均为原来的2010倍.
的坐标在一条射线上,其横纵坐标均为原来的2010倍.解答:解:(1)在△OB
 C
C 中,
中,∵OB
 =1,B
=1,B C
C =
= ,
,∴tan∠C
 OB
OB =
= ,
,∴∠C
 OB
OB =60°,OC
=60°,OC =2,
=2,∵OB
 =mOB
=mOB ,OB
,OB =OC
=OC ,
,∴m=2,
故答案为2;
(2)∵每一次的旋转角是60°,
∴旋转6次后C在x轴正半轴上,
∴2011÷6=335…1,
∴点C
 的坐标跟C
的坐标跟C 的坐标在一条射线上,
的坐标在一条射线上,∵第2次旋转后,各边长是原来的2倍,第3次旋转后,各边长是原来的22倍,
∴点C
 的横纵坐标均为原来的2010倍.
的横纵坐标均为原来的2010倍.故答案为(
 ).
).点评:考查规律旋转后点的坐标;得到所求点的位置是解决本题的突破点;得到坐标的规律是解决本题的难点

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC
α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC
 =
= °,∠
°,∠ =
= °,那么∠
°,那么∠ = °
= °


 绕点
绕点 按顺时针方向旋转到
按顺时针方向旋转到 的位置,其中
的位置,其中 交直线
交直线 于点
于点 ,
, 分别交直线
分别交直线 于点
于点 ,则旋转后的图中,全等三角形共有( )
,则旋转后的图中,全等三角形共有( )
