题目内容
某单位为了响应政府发出的“全民健身”的号召,打算在长和宽分别为20米和16米的矩形大厅内修建一个40平方米的矩形健身房ABCD,该健身房的四面墙壁中有两面沿用大厅的旧墙壁(如图为平面示意图),且每面旧墙壁上所沿用的旧墙壁长度不得超过其长度的一半,己知装修旧墙壁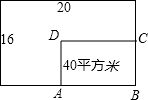 的费用为20元/平方米,新建(含装修)墙壁的费用为80元/平方米,设健身房高3米,健身房AB的长为x米,BC的长为y米,修建健身房墙壁的总投资为w元.
的费用为20元/平方米,新建(含装修)墙壁的费用为80元/平方米,设健身房高3米,健身房AB的长为x米,BC的长为y米,修建健身房墙壁的总投资为w元.
(1)求y与x的函数关系式,并写出自变量x的范围.
(2)求w与x的函数关系,并求出当所建健身房AB长为8米时总投资为多少元?
解:(1)根据题意可知 ,
,
∵
∴5≤x≤10
(2)根据题可知w=(x+ )×3×80+(x+
)×3×80+(x+ )×3×20=300×(x+
)×3×20=300×(x+ ),
),
当x=8时, (元).
(元).
分析:(1)解析式相对简单,自变量取值范围只需根据“所沿用的旧墙壁长度不得超过其长度的一半”即可求出.
(2)总投资有两部分构成,旧墙和新建墙,应该根据(1)中结果,把这两部分用含x的式子分别表示出来,即可求解.
点评:此题主要考查反比例函数在实际生活中的应用,解题关键是把实际问题转化为数学问题,抽象到反比例函数中.
 ,
,∵

∴5≤x≤10
(2)根据题可知w=(x+
 )×3×80+(x+
)×3×80+(x+ )×3×20=300×(x+
)×3×20=300×(x+ ),
),当x=8时,
 (元).
(元).分析:(1)解析式相对简单,自变量取值范围只需根据“所沿用的旧墙壁长度不得超过其长度的一半”即可求出.
(2)总投资有两部分构成,旧墙和新建墙,应该根据(1)中结果,把这两部分用含x的式子分别表示出来,即可求解.
点评:此题主要考查反比例函数在实际生活中的应用,解题关键是把实际问题转化为数学问题,抽象到反比例函数中.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 (含装修)墙壁的费用为80元/m2.设健身房的高为3m,一面旧墙壁AB的长为xm,修建健身房墙壁的总投入为y元.
(含装修)墙壁的费用为80元/m2.设健身房的高为3m,一面旧墙壁AB的长为xm,修建健身房墙壁的总投入为y元. 的费用为20元/平方米,新建(含装修)墙壁的费用为80元/平方米,设健身房高3米,健身房AB的长为x米,BC的长为y米,修建健身房墙壁的总投资为w元.
的费用为20元/平方米,新建(含装修)墙壁的费用为80元/平方米,设健身房高3米,健身房AB的长为x米,BC的长为y米,修建健身房墙壁的总投资为w元.
