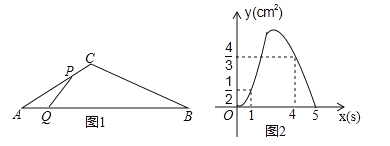��Ŀ����
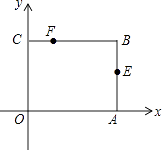
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У��ı���![]() �����������ֱ�Ϊ
�����������ֱ�Ϊ![]() ������
������![]() ��
��![]() ͬʱ��
ͬʱ��![]() ��������˶�ʱ��Ϊ
��������˶�ʱ��Ϊ![]() �룬��
�룬��![]() ��
��![]() ������
������![]() ��λ����/����ٶ����
��λ����/����ٶ����![]() �˶�����
�˶�����![]() ������
������![]() �˶�����
�˶�����![]() ���˶����ٶȷֱ�Ϊ
���˶����ٶȷֱ�Ϊ![]() ����λ����/�룩.��
����λ����/�룩.��![]() �е�һ�㵽��
�е�һ�㵽��![]() ��ʱ������ͬʱֹͣ�˶�.
��ʱ������ͬʱֹͣ�˶�.
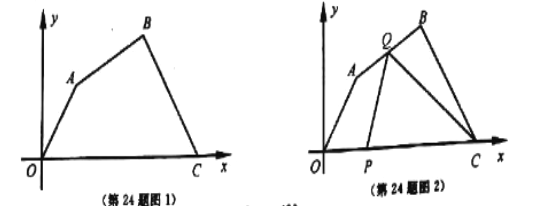
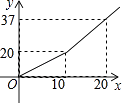
��1����![]() ����ֱ�ߵĺ�������ʽ��
����ֱ�ߵĺ�������ʽ��
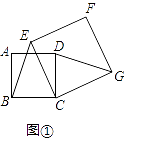
��2����ͼ2������![]() ��
��![]() ���˶�ʱ����
���˶�ʱ����![]() �����
�����![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��![]() �����ֵ��
�����ֵ��
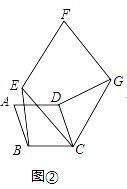
��3����![]() ��
��![]() ���˶������У����߶�
���˶������У����߶�![]() �Ĵ�ֱƽ���߾����ı���
�Ĵ�ֱƽ���߾����ı���![]() �Ķ��㣬����Ӧ��
�Ķ��㣬����Ӧ��![]() ֵ.
ֵ.
���𰸡�(1) y=![]() x+2
x+2![]() ;(2)
;(2) ![]() ,��t=5ʱ��S�����ֵ�����ֵΪ
,��t=5ʱ��S�����ֵ�����ֵΪ![]() ;(3) t��ֵΪ
;(3) t��ֵΪ![]() .
.
��������
�����������1���ô���ϵ������ֱ��AB�Ľ���ʽ���ɣ���2�����������ε������ʽ�õ�����t�Ķ�������ʽ�����ɶ��κ���ͼ����������S�����ֵ���ɣ���3������t��ֵ��������ۣ��������г���ͬ�ķ��̴Ӷ����t��ֵ.
���������
��1���⣺��A��3��3 ����B��9��5 ������y=kx+b,
�� 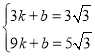 ;
;
��ã�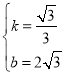 ;
;
��y=![]() x+2
x+2![]() ;
;
��2���⣺����PQC�У�PC=14-t,PC���ϵĸ��߳�Ϊ![]() ;
;
��![]()
����t=5ʱ��S�����ֵ�����ֵΪ![]() .
.
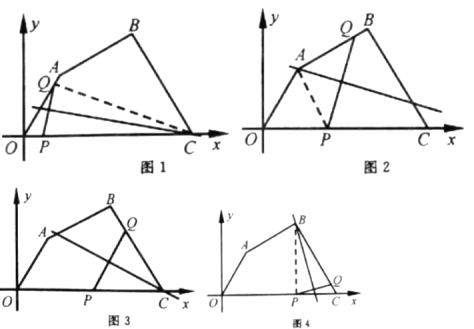
��3���⣺ a.��0��t��2ʱ���߶�PQ���д��߾�����C����ͼ1����
�ɵ÷���![]()
��ã�![]() ����ȥ������ʱt=
����ȥ������ʱt=![]() .
.
b.��2��t��6ʱ���߶�PQ���д��߾�����A����ͼ2��
�ɵ÷���![]() ,
,
��ã�![]() ����ȥ������ʱ
����ȥ������ʱ![]() ��
��
c.��6��t��10ʱ��
���߶�PQ���д��߾�����C����ͼ3��
�ɵ÷���14-t=25-![]() ;
;
��ã�t=![]() .
.
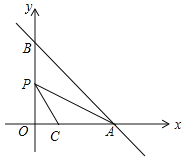
���߶�PQ���д��߾�����B����ͼ4��
�ɵ÷���![]() ;
;
���![]() ����ȥ����
����ȥ����
��ʱ![]() ��
��
����������t��ֵΪ![]() .
.

 ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�����Ŀ����ij�������У������������m��v֮���4���Ӧ�������±���
m | 1 | 2 | 3 | 4 |
v | 0.01 | 2.9 | 8.03 | 15.1 |
��m��v֮��Ĺ�ϵ��ӽ������и���ϵʽ�е�( )
A. v��2m��1B. v��m2��1C. v��3m��3D. v��m��1