题目内容
在边长为1的菱形ABCD中，0°＜∠A＜90°，设∠A=α，则菱形的面积S与α的函数关系式为
- A.S=sinα
- B.S=cosα
- C.S=tanα
- D.S=
A
分析：根据菱形的面积=底边×高，底边为1，高为sinα，继而即可选出答案．
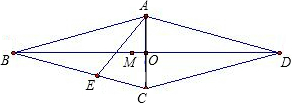
解答：过点D作DE⊥AB，如下图所示：
则DE=AD•sinα=sinα，
∴菱形的面积=AB•DE=1•sinα=sinα．
故选A．
点评：本题考查菱形的性质，属于基础题，比较容易解答，关键是掌握菱形的面积公式．
分析：根据菱形的面积=底边×高，底边为1，高为sinα，继而即可选出答案．
解答：过点D作DE⊥AB，如下图所示：
则DE=AD•sinα=sinα，
∴菱形的面积=AB•DE=1•sinα=sinα．
故选A．
点评：本题考查菱形的性质，属于基础题，比较容易解答，关键是掌握菱形的面积公式．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
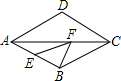如图，在边长为6的菱形ABCD中，∠DAB=60°，E为AB的中点，F是AC上的一动点，则EF+BF的最小值为
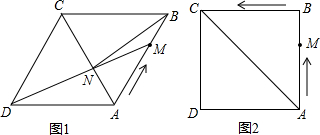C的路线向终点C运动，连接DM交AC于点N，连接BN．
在边长为6的菱形ABCD中，动点M从点A出发，沿A?B?C向终点C运动，连接DM交AC于点N．