题目内容
 如图,在直角坐标系中,△ABO的顶点A的坐标为(6,0),AB=8,∠BA0=60°.请作出△ABO绕A顺时针旋转60°后形成的△AB′0′,并求△AB′O′的边B′O′所在直线的解析式.
如图,在直角坐标系中,△ABO的顶点A的坐标为(6,0),AB=8,∠BA0=60°.请作出△ABO绕A顺时针旋转60°后形成的△AB′0′,并求△AB′O′的边B′O′所在直线的解析式.考点:作图-旋转变换,待定系数法求一次函数解析式
专题:
分析:根据旋转的性质,作∠BAB′=60°,然后截取AB′=AB,在AB上截取AO′=AO,然后顺差连接AB′O′即可得到△AB′O′,过点O′作O′C⊥x轴于C,过点B′作B′D⊥x轴于D,然后解直角三角形求出点O′、B′的坐标,再利用待定系数法求一次函数解析式解答.
解答: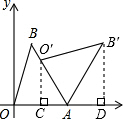 解:△AB′0′如图所示;
解:△AB′0′如图所示;
过点O′作O′C⊥x轴于C,过点B′作B′D⊥x轴于D,
∵A(6,0),
∴AO=6,
由旋转的性质得,AO′=AO=6,AB′=AB=8,
∵∠BA0=60°,
∴AC=
AO′=
×6=3,
∴OC=AO-AC=6-3=3,
由勾股定理得,O′C=
=3
,
∴点O′的坐标为(3,3
),
∵旋转角为60°,∠BAO=60°,
∴∠BAD=180°-60°×2=60°,
∴AD=
AB′=
×8=4,
∴OD=AO+AD=6+4=10,
由勾股定理得,B′D=
=4
,
∴点B′的坐标为(10,4
),
设直线O′B′的解析式为y=kx+b,
则
,
解得
,
所以,直线B′O′的解析式为y=
x+
.
 解:△AB′0′如图所示;
解:△AB′0′如图所示;过点O′作O′C⊥x轴于C,过点B′作B′D⊥x轴于D,
∵A(6,0),
∴AO=6,
由旋转的性质得,AO′=AO=6,AB′=AB=8,
∵∠BA0=60°,
∴AC=
| 1 |
| 2 |
| 1 |
| 2 |
∴OC=AO-AC=6-3=3,
由勾股定理得,O′C=
| 62-32 |
| 3 |
∴点O′的坐标为(3,3
| 3 |
∵旋转角为60°,∠BAO=60°,
∴∠BAD=180°-60°×2=60°,
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
∴OD=AO+AD=6+4=10,
由勾股定理得,B′D=
| 82-42 |
| 3 |
∴点B′的坐标为(10,4
| 3 |
设直线O′B′的解析式为y=kx+b,
则
|
解得
|
所以,直线B′O′的解析式为y=
| ||
| 7 |
18
| ||
| 7 |
点评:本题考查了利用旋转变换作图,待定系数法求一次函数解析式,解直角三角形,熟练掌握旋转的性质是解题得解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若|x-3|+(y+3)2=0,则yx=( )
| A、-9 | B、9 | C、-27 | D、27 |
方程2x2+3x=0解是( )
| A、x1=0,x2=-3 | ||
B、x1=0,x2=
| ||
C、x1=0,x2=-
| ||
D、x1=0,x2=-
|
 已知抛物线y=ax2+bx+c经过A(-1,0)、B(2,0)、C(0,2)三点.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(2,0)、C(0,2)三点. 如图,是一个10×10正方形网格纸,△ABC中A点的坐标为(2,4),B点的坐标为(1,1).
如图,是一个10×10正方形网格纸,△ABC中A点的坐标为(2,4),B点的坐标为(1,1). 在数轴上表示下列数,并用“<”号把这些数连接起来.
在数轴上表示下列数,并用“<”号把这些数连接起来.