题目内容
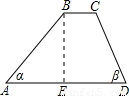
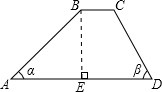 如图,一防洪拦水坝的横断面为梯形ABCD,坝顶宽BC=3米,坝高BE=6米,坡角α为45°,坡角β为63°,求横断面(梯形ABCD)的面积.
如图,一防洪拦水坝的横断面为梯形ABCD,坝顶宽BC=3米,坝高BE=6米,坡角α为45°,坡角β为63°,求横断面(梯形ABCD)的面积.
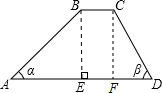 解:过点C作CF⊥AD于点F,
解:过点C作CF⊥AD于点F,∵BC∥AD,BE是高,
∴四边形BCFE是矩形,
∴EF=BC=3米,CF=BE=6米,
在Rt△ABE中,∠A=α=45°,
∴AE=BE=6米,
在Rt△CDF中,DF=
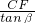 =
=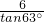 ≈3.06(米),
≈3.06(米),∴AD=AE+EF+DF=12.06(米),
∴横断面(梯形ABCD)的面积为:
 (BC+AD)•BE=
(BC+AD)•BE= ×(3+12.06)×6=45.18(米2).
×(3+12.06)×6=45.18(米2).分析:首先过点C作CF⊥AD于点F,易得四边形BCFE是矩形,即可求得EF与CF的长,又由坡角α为45°,坡角β为63°,利用三角函数的知识即可求得AE与DF的长.
点评:此题考查了坡度坡角问题与梯形的性质.此题难度不大,能构造直角三角形,并能借助于解直角三角形的知识求解是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
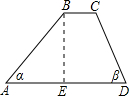
 (2012•黄冈模拟)如图,一防洪拦水坝的横断面为梯形ABCD,坝顶宽BC=3米,坝高BE=6米,坡角α为45°,坡角β为63°,求横断面(梯形ABCD)的面积.
(2012•黄冈模拟)如图,一防洪拦水坝的横断面为梯形ABCD,坝顶宽BC=3米,坝高BE=6米,坡角α为45°,坡角β为63°,求横断面(梯形ABCD)的面积.
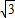 kx+k2-k+2=0,判别这个方程根的情况.”一题的解答过程,请你判断其是否正确,若有错误,请你写出正确解答.
kx+k2-k+2=0,判别这个方程根的情况.”一题的解答过程,请你判断其是否正确,若有错误,请你写出正确解答.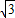 k)2-4×1×(k2-k+2)
k)2-4×1×(k2-k+2)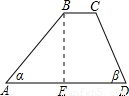
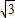 kx+k2-k+2=0,判别这个方程根的情况.”一题的解答过程,请你判断其是否正确,若有错误,请你写出正确解答.
kx+k2-k+2=0,判别这个方程根的情况.”一题的解答过程,请你判断其是否正确,若有错误,请你写出正确解答.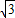 k)2-4×1×(k2-k+2)
k)2-4×1×(k2-k+2)