Question

【题目】(1)已知a＋b＝7，ab＝10，求a2＋b2，(a－b)2的值；

(2)先化简(-)÷，并回答：原代数式的值可以等于－1吗？为什么？

Answer 1

【答案】(1)a2＋b2＝29， (a－b)2＝9；(2)原代数式的值不能等于－1，理由见解析.

【解析】试题分析：（1）根据完全平方公式，即可解答；

（2）原式括号中两项约分后，利用乘法分配律化简，约分后利用同分母分式的减法法则计算得到最简结果，令原式的值为-1，求出x的值，代入原式检验即可得到结果．

试题解析：(1)a2＋b2＝(a＋b)2－2ab＝72－2×10＝49－20＝29， (a－b)2＝(a＋b)2－4ab＝72－4×10＝49－40＝9.

(2) 原式=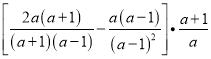

=

=，

原式的值为-1，即=-1，

去分母得：a+1=-a+1，

解得：a=0，

代入原式检验，分母为0，不合题意，

则原式的值不可能为-1．