题目内容
抛物线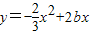
与x轴的两个不同交点是点O和点A，顶点B在直线
上，则关于△OAB的判断正确的是（ ）A．等腰三角形
B．直角三角形
C．等边三角形
D．等腰直角三角形
【答案】分析：利用二次函数的顶点式公式，即可得出顶点B的坐标，代入直线中，即可得出b的值，从而可得出O点和A点在坐标，利用由三角函数求角BOA的度数，即可判断△OAB的形状．
解答：解：抛物线
，
即顶点B的坐标为（
b，-
b2），
代入直线
中，
得-
b2=
，
得b=-
，b=0（舍去），
即可得出O（0，0）、A（-
，0），B（-
，-
）；
OB=1，可得∠ABO=120°；
根据抛物线的对称性，可知BA=BO；
故△BOA为等腰三角形．
故选A．
点评：本题主要考查了抛物线的性质及其顶点坐标公式的使用，本题具有一定的综合性，需要同学们理清题意，认真完成题目．
解答：解：抛物线
，即顶点B的坐标为（
b，-b2），代入直线
中，得-
b2=，得b=-
，b=0（舍去），即可得出O（0，0）、A（-
，0），B（-，-）；OB=1，可得∠ABO=120°；
根据抛物线的对称性，可知BA=BO；
故△BOA为等腰三角形．
故选A．
点评：本题主要考查了抛物线的性质及其顶点坐标公式的使用，本题具有一定的综合性，需要同学们理清题意，认真完成题目．
练习册系列答案
阅读快车系列答案
相关题目
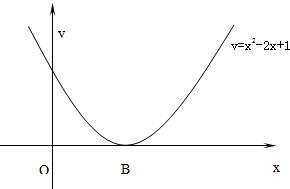7、已知抛物线y=a（x-t-1）2+t2（a，t是常数，a≠0，t≠0）的顶点是A，抛物线y=x2-2x+1的顶点是B．
（2007•郑州模拟）如图，已知直线y=-x+2与坐标轴交于A、B两点，点P在x轴上．