题目内容
等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
△APQ是等边三角形
解析试题分析:由△ABP≌△ACQ得AP=AQ,再证∠PAQ=60°即可.
因为△ABC是等边三角形,在△ABP和△ACQ中,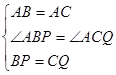
所以△ABP≌△ACQ
所以AP=AQ,∠BAP=∠CAQ。所以△APQ是等边三角形.
答对2分,证明出全等三角形4分,证明正确4分
考点:本题考查三角形的判定以及性质的应用。
点评:解析几何的求解,需要对图形整体把握,可以根据已知条件确定能得出的结论,进而一步步与所要求解的对象建立联系。

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
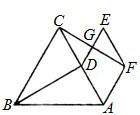 22、如图,在等边△ABC中,点D为AC中点,以AD为边作菱形ADEF,且AF∥BC,连接FC交DE于点G.
22、如图,在等边△ABC中,点D为AC中点,以AD为边作菱形ADEF,且AF∥BC,连接FC交DE于点G. 14、如图,在等边△ABC中,点D、E分别在边BC,AB上,且BD=AE,AD与CE交于点F.则∠DFC=
14、如图,在等边△ABC中,点D、E分别在边BC,AB上,且BD=AE,AD与CE交于点F.则∠DFC= 26、如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.
26、如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.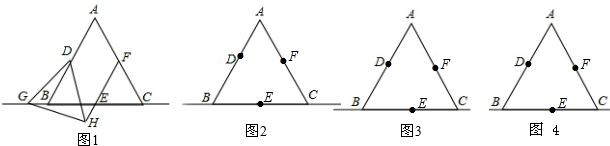
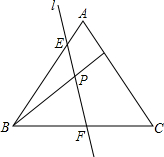 如图,在等边△ABC中,点D为AC上一点,连结AB,BD,BC分别相交于点E,P,F,且∠BPF=60°
如图,在等边△ABC中,点D为AC上一点,连结AB,BD,BC分别相交于点E,P,F,且∠BPF=60°