题目内容
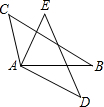 如图,在△CAB和△EAD中,∠CAE=∠BAD,BC=DE.
如图,在△CAB和△EAD中,∠CAE=∠BAD,BC=DE.(1)请你选择以下条件:①AB=AD;②∠C=∠E;③∠B=∠D;④∠CAB=∠EAD中的一个条件,使得△CAB≌△EAD,并说明理由.(只要选一种即可)
(2)在(1)的前提下,若AB=
| 12 |
| x-2 |
| 72 |
| x2-4 |
| 7 |
| 2 |
①分别求出x,y的值;
②化简:
| 1 |
| xy |
| 1 |
| (x+4)(y+4) |
| 1 |
| (x+8)(y+8) |
| 1 |
| (x+12)(y+12) |
| 1 |
| (x+4n)(y+4n) |
(n为正整数)
分析:(1)可以选择②,然后根据已知条件求出∠CAB=∠EAD,再利用AAS定理从而证得△CAB≌△EAD;
(2)根据①可得AB=AD,即
=
,然后解出x的值,利用此方法依次求出BC=DE或AC=AE,从而解出x的值,再由三角形三边关系判断是否合题意,最后得出正确答案,x=4,y=8.②把x、y的值代入方程,然后展开化简即可.
(2)根据①可得AB=AD,即
| 12 |
| x-2 |
| 72 |
| x2-4 |
解答:解:(1)可以选择②∠C=∠E或③∠B=∠D,中的一种.
∵在△CAB和△EAD中,∠CAE=∠BAD,BC=DE,
∴∠CAB=∠EAD,
又∵∠C=∠E,
∴△CAB≌△EAD(利用“AAS”)
(2)①由(1)得AB=AD,
=
,
解得x=4,
经检验x=4是原方程的根,所以x=4;
或(BC=DE)2x-y+7=
x-y+1解得x=4;
或(AC=AE)由(y-6)2=4,解得y=8或4;
当x=4,y=8时,AB=AD=6,BC=DE=7,AC=AE=4;
当x=4,y=4时,AB=AD=6,BC=DE=11,AC=AE=4,此时三角形不能构成,因此不合题意.
所以x=4,y=8.
②当x=4,y=8时,原式=
+
+
+
+…+
,
=
[
+
+
+…+
]
=
(1-
+
-
+
-
+…+
-
)
=
(1-
)=
.
∵在△CAB和△EAD中,∠CAE=∠BAD,BC=DE,
∴∠CAB=∠EAD,
又∵∠C=∠E,
∴△CAB≌△EAD(利用“AAS”)
(2)①由(1)得AB=AD,
| 12 |
| x-2 |
| 72 |
| x2-4 |
解得x=4,
经检验x=4是原方程的根,所以x=4;
或(BC=DE)2x-y+7=
| 7 |
| 2 |
或(AC=AE)由(y-6)2=4,解得y=8或4;
当x=4,y=8时,AB=AD=6,BC=DE=7,AC=AE=4;
当x=4,y=4时,AB=AD=6,BC=DE=11,AC=AE=4,此时三角形不能构成,因此不合题意.
所以x=4,y=8.
②当x=4,y=8时,原式=
| 1 |
| 4×8 |
| 1 |
| 8×12 |
| 1 |
| 12×16 |
| 1 |
| 16×20 |
| 1 |
| (4n+4)(4n+8) |
=
| 1 |
| 16 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| (n+1)(n+2) |
=
| 1 |
| 16 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 1 |
| 16 |
| 1 |
| n+2 |
| n+1 |
| 16n+32 |
点评:本题考查三角形全等的判定方法、有理数的混合运算、解分式方程以及三角形三边关系;在判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
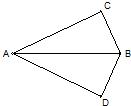 5、如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”证明△ABC≌△ABD,则需要加条件
5、如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”证明△ABC≌△ABD,则需要加条件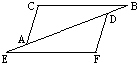 11、如图,在△ABC和△DEF,AC=DF,AE=BD,当添加条件
11、如图,在△ABC和△DEF,AC=DF,AE=BD,当添加条件 如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”证明△ABC≌△ABD,则需要加条件
如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”证明△ABC≌△ABD,则需要加条件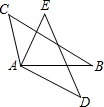 如图,在△CAB和△EAD中,∠CAE=∠BAD,BC=DE.
如图,在△CAB和△EAD中,∠CAE=∠BAD,BC=DE. ,BC=2x-y+7,AC=(y-6)2,AD=
,BC=2x-y+7,AC=(y-6)2,AD=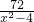 ,DE=
,DE=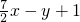 ,AE=4,请解决以下问题:
,AE=4,请解决以下问题: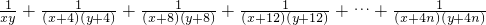 .
.