题目内容
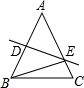 已知,在△ABC中,AB=AC=32cm,DE垂直平分AB交AC于E.
已知,在△ABC中,AB=AC=32cm,DE垂直平分AB交AC于E.
(1)∠A=50°,则∠EBC=______°;
(2)若BC=21cm,则△BCE的周长是______.
解:(1)∵DE垂直平分AB交AC于E,
∴AE=BE,
∵∠A=50°,
∴∠ABE=∠A=50°,
∵AB=AC,
∴∠ABC=∠C= =65°,
=65°,
∴∠EBC=∠ABC-∠ABE=65°-50°=15°;
(2)∵AB=AC=32cm,BC=21cm,
∴△BCE的周长是:BC+BE+EC=BC+_AE+EC=BC+AC=21+32=53(cm).
故答案为:(1)15,(2)53cm.
分析:(1)由DE垂直平分AB交AC于E,可得AE=BE,然后由等腰三角形的性质,可求得∠ABE的度数,又由AB=AC,∠ABC的度数,继而求得答案;
(2)由AB=AC=32cm,BC=21cm,△BCE的周长=AC+BC,即可求得答案.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.
∴AE=BE,
∵∠A=50°,
∴∠ABE=∠A=50°,
∵AB=AC,
∴∠ABC=∠C=
 =65°,
=65°,∴∠EBC=∠ABC-∠ABE=65°-50°=15°;
(2)∵AB=AC=32cm,BC=21cm,
∴△BCE的周长是:BC+BE+EC=BC+_AE+EC=BC+AC=21+32=53(cm).
故答案为:(1)15,(2)53cm.
分析:(1)由DE垂直平分AB交AC于E,可得AE=BE,然后由等腰三角形的性质,可求得∠ABE的度数,又由AB=AC,∠ABC的度数,继而求得答案;
(2)由AB=AC=32cm,BC=21cm,△BCE的周长=AC+BC,即可求得答案.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上. (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.