题目内容
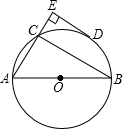
在Rt△ABC中,BC=9,CA=12,∠ABC的平分线BD交AC与点D,DE⊥DB交AB于点E.
(1)设⊙O是△BDE的外接圆,求证:AC是⊙O的切线;
(2)设⊙O交BC于点F,连接EF,求
的值.

(1)设⊙O是△BDE的外接圆,求证:AC是⊙O的切线;
(2)设⊙O交BC于点F,连接EF,求
| EF |
| AC |

(1)证明:∵DE⊥DB,⊙O是Rt△BDE的外接圆
∴BE是⊙O的直径,点O是BE的中点,连接OD(1分)
∵∠C=90°
∴∠DBC+∠BDC=90°
又∵BD为∠ABC的平分线
∴∠ABD=∠DBC
∵OB=OD
∴∠ABD=∠ODB
∴∠ODB+∠BDC=90°
∴∠ODC=90°(4分)
又∵OD是⊙O的半径
∴AC是⊙O的切线(5分)
(2)设⊙O的半径为r,
在Rt△ABC中,AB2=BC2+CA2=92+122=225
∴AB=15(7分)
∵∠A=∠A,∠ADO=∠C=90°
∴△ADO∽△ACB.
∴
=
∴
=
∴r=
∴BE=2r=
,(10分)
又∵BE是⊙O的直径
∴∠BFE=90°
∴△BEF∽△BAC
∴
=
=
=
(12分)

∴BE是⊙O的直径,点O是BE的中点,连接OD(1分)
∵∠C=90°
∴∠DBC+∠BDC=90°
又∵BD为∠ABC的平分线
∴∠ABD=∠DBC
∵OB=OD
∴∠ABD=∠ODB
∴∠ODB+∠BDC=90°
∴∠ODC=90°(4分)
又∵OD是⊙O的半径
∴AC是⊙O的切线(5分)
(2)设⊙O的半径为r,
在Rt△ABC中,AB2=BC2+CA2=92+122=225
∴AB=15(7分)
∵∠A=∠A,∠ADO=∠C=90°
∴△ADO∽△ACB.
∴
| AO |
| AB |
| OD |
| BC |
∴
| 15-r |
| 15 |
| r |
| 9 |
∴r=
| 45 |
| 8 |
∴BE=2r=
| 45 |
| 4 |
又∵BE是⊙O的直径
∴∠BFE=90°
∴△BEF∽△BAC
∴
| EF |
| AC |
| BE |
| BA |
| ||
| 15 |
| 3 |
| 4 |


练习册系列答案
相关题目


 O1于点E.
O1于点E.