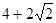题目内容
已知,如图,直线l经过A(4,0)和B(0,4)两点,它与抛物线y=ax2在第一象限内相交于点P,又知△AOP的面积为4,求a的值.
【答案】分析:依题意可得P是AB的中点,推出△OAP是等腰直角三角形后易得a值.
解答: 解:∵OA=OB=4,
解:∵OA=OB=4,
∴△AOB的面积为8,
又∵△AOP的面积为4,
∴AP= AB,
AB,
∴P是AB的中点,
从而可得△OAP是等腰直角三角形,过P作PC⊥OA于C,可得P(2,2),
将P(2,2)代入y=ax2中,得a= .
.
点评:本题考查的是三角形的性质以及二次函数与图象相结合的应用,难度中等.
解答:
 解:∵OA=OB=4,
解:∵OA=OB=4,∴△AOB的面积为8,
又∵△AOP的面积为4,
∴AP=
 AB,
AB,∴P是AB的中点,
从而可得△OAP是等腰直角三角形,过P作PC⊥OA于C,可得P(2,2),
将P(2,2)代入y=ax2中,得a=
 .
.点评:本题考查的是三角形的性质以及二次函数与图象相结合的应用,难度中等.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 已知:如图,直线y=-x+4分别与x轴,y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )
已知:如图,直线y=-x+4分别与x轴,y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( ) 分别与
分别与 轴,
轴, 轴交于
轴交于 两点,从点
两点,从点 射出的光线经直线
射出的光线经直线 反射后再射到直线
反射后再射到直线 上,最后经直线
上,最后经直线 点,则光线所经过的路程是( )
点,则光线所经过的路程是( )




 分别与
分别与 轴,
轴, 轴交于
轴交于 两点,从点
两点,从点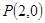 射出的光线经直线
射出的光线经直线 反射后再射到直线
反射后再射到直线 上,最后经直线
上,最后经直线 点,则光线所经过的路程是( )
点,则光线所经过的路程是( ) B.
B.
 C.
C. D.
D. 

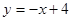 分别与
分别与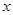 轴,
轴,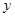 轴交于
轴交于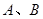 两点,从点
两点,从点 射出的光线经直线
射出的光线经直线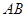 反射后再射到直线
反射后再射到直线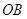 上,最后经直线
上,最后经直线 点,则光线所经过的路程是( )
点,则光线所经过的路程是( )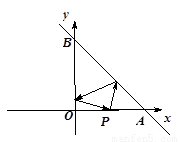
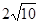 B.
B. 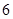 C.
C. D.
D.