题目内容
 如图,EF为正方形ABCD的对折线,将∠A沿DK折叠使它的顶点A落在EF上的G点,则∠DKG为( )
如图,EF为正方形ABCD的对折线,将∠A沿DK折叠使它的顶点A落在EF上的G点,则∠DKG为( )| A、15° | B、30° | C、55° | D、75° |
分析:先根据正方形的性质及翻折不变性的原则求出∠DFG的度数,再求出∠GDF的度数,进而可求出∠KDG的度数,再由直角三角形的性质即可解答.
解答:解:∵EF为正方形ABCD的对折线,
∴AD=2DF,
∵△GDK是△ADK沿DK对折而成,
∴∠DAK=∠DGK=90°,∠ADK=∠GDK,AD=GD,
∴GD=2DF,
∴∠DGF=30°,∠GDF=60°,∠ADG=30°,
∵∠DAK=∠DGK=90°,∠ADK=∠GDK,
∴∠KDG=
∠ADG=
×30°=15°,
∴∠DKG=90°-∠KDG=75°.
故答案为:D.
∴AD=2DF,
∵△GDK是△ADK沿DK对折而成,
∴∠DAK=∠DGK=90°,∠ADK=∠GDK,AD=GD,
∴GD=2DF,
∴∠DGF=30°,∠GDF=60°,∠ADG=30°,
∵∠DAK=∠DGK=90°,∠ADK=∠GDK,
∴∠KDG=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DKG=90°-∠KDG=75°.
故答案为:D.
点评:本题考查的是正方形的性质及翻折不变性的性质,解答此题的关键是熟知折叠的性质,即折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.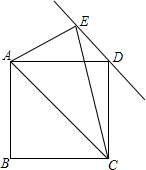 如图,AC为正方形ABCD的对角线,DE∥AC,且CE=AC
如图,AC为正方形ABCD的对角线,DE∥AC,且CE=AC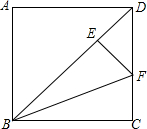 如图,E为正方形ABCD的对角线BD上一点,且BE=BC,点F在CD上,且EF⊥BD.
如图,E为正方形ABCD的对角线BD上一点,且BE=BC,点F在CD上,且EF⊥BD.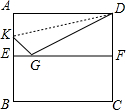 如图,EF为正方形ABCD的对折线,将∠A沿DK折叠使它的顶点A落在EF上的G点,则∠DKG为
如图,EF为正方形ABCD的对折线,将∠A沿DK折叠使它的顶点A落在EF上的G点,则∠DKG为