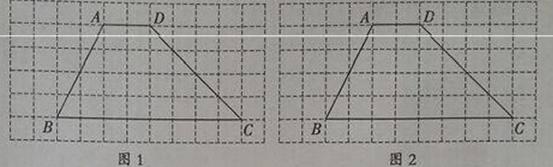题目内容
22.如图,将□A BCD的边DC延长到点E,使CE=DC,连接AE,
BCD的边DC延长到点E,使CE=DC,连接AE,
交BC于点F.
⑴求证:△ABF≌△ECF;
⑵若∠AFC=2∠D ,连接AC、BE.求证:四边形ABEC是矩形.
,连接AC、BE.求证:四边形ABEC是矩形.
 |
证明:⑴∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.∴∠ABF=∠ECF.
∵EC=DC, ∴AB=EC.
在△ABF和△ECF中,∵∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,
∴△ABF≌△ECF. 
(2)解法一:∵AB=EC ,AB∥EC,
∴四边形ABEC是平行四边形.∴AF=EF, BF=CF.
∵四边形ABCD是平行四边形,∴∠ABC=∠D,
又∵∠AFC=2∠D,∴∠AFC=2∠ABC.
∵∠AFC=∠ABF+∠BAF,∴∠ABF=∠BAF.∴FA=FB.
∴FA=FE=FB=FC, ∴AE=BC.∴□ABEC是矩形.
解法二:∵AB=EC ,AB∥EC,∴四边形ABEC是平行四边形.
∵四边形ABCD是平行四边形,∴AD∥BC,∴∠D=∠BCE.
又∵∠AFC=2∠D,∴∠AFC=2∠BCE,
∵∠AFC=∠FCE+∠FEC,∴∠ FCE=∠FEC.∴∠D=∠FEC.∴AE=AD.
FCE=∠FEC.∴∠D=∠FEC.∴AE=AD.
又∵CE=DC,∴AC⊥DE.即∠ACE=90°.
∴□ABEC是矩形.

将6.18×10﹣3化为小数的是( )
|
| A. | 0.000618 | B. | 0.00618 | C. | 0.0618 | D. | 0.618 |
 无解,则实数a的取值范围是( )
无解,则实数a的取值范围是( ) x+b的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-
x+b的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-
 有意义,则实数x的取值范围是
有意义,则实数x的取值范围是 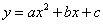 的图象的一部分,对称轴是直线X=1
的图象的一部分,对称轴是直线X=1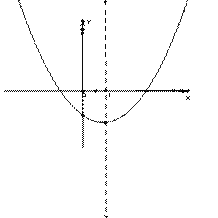
 1)在图1中画一个与梯形ABCD面积相等,且以CD为边的三角形;
1)在图1中画一个与梯形ABCD面积相等,且以CD为边的三角形;