Question

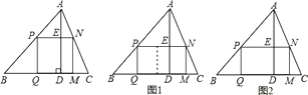
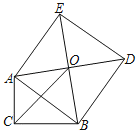
【题目】如图所示，在Rt△ABC中，∠ACB＝90°，以斜边AB为边向外作正方形ABDE，且正方形的对角线交于点O，连接OC．已知AC＝5，OC＝12，则另一直角边BC的长为_____．（提示：分别过O向CA、CB作垂线）

Answer 1

【答案】7

【解析】

过点O作OF⊥BC，过点A作AM⊥OF，根据正方形的性质得出∠AOB＝90°，OA＝OB，求出∠BOF＝∠OAM，根据AAS证明△AOM≌△OBF，得出AM＝OF，OM＝FB，进而可得等腰三角形OCF，根据勾股定理求出CF＝OF＝6，求出BF，即可求出答案．

解：过点O作OF⊥BC于F，过点A作AM⊥OF于M，

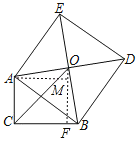
∵∠AMO＝∠OFB＝90°，∠ACB＝∠CFM＝∠AMF＝90°，

∴四边形ACFM是矩形，

∴AM＝CF，AC＝MF＝5，

∵四边形ABDE为正方形，

∴∠AOB＝90°，OA＝OB，

∴∠AOM+∠BOF＝90°，

又∵∠AMO＝90°，

∴∠AOM+∠OAM＝90°，

∴∠BOF＝∠OAM，

在△AOM和△OBF中，，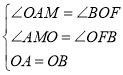

∴△AOM≌△OBF（AAS），

∴AM＝OF，OM＝FB，

∴OF＝CF，

∵∠CFO＝90°，

∴△CFO是等腰直角三角形，

∵OC＝12，

∴由勾股定理得：CF＝OF＝6，

∴BF＝OM＝OF﹣FM＝6﹣5＝，

∴BC＝CF+BF＝6+＝7．

故答案为：7．