题目内容
当x变化时,|x-5|+|x+t|有最小值2,则常数t的值为______.
【答案】分析:把|x-5|、|x+t|分正负情况讨论,比如:++、--,+-,-+,进行分析,进而得出结论.
解答:解:(1)当这两个都为负数时,
则:|x-5|+|x+t|=2,变为:-x+5-x-t=2,
可得:t=-2x+3,这时x为变量,则t也为变量,与题意不符;
(2)当这两个都为正数时,
则:|x-5|+|x+t|=2,变为:x-5+x-t=2,
可得:t=2x-7,这时x为变量,则t也为变量,与题意不符;
(3)当|x-5|为正数、|x+t|负数时,
则:|x-5|+|x+t|=2,变为:x-5-x-t=2,
可得:t=-7,这时x为变量,则t为定值,符合题意;
(4)当|x-5|为负数、|x+t|正数时,
则:|x-5|+|x+t|=2,变为:-x+5+x+t=2,
可得:t=-3,这时x为变量,则t为定值,符合题意;
故答案为:-3或-7.
点评:此题主要考查了绝对值的性质,解答此题应结合题意,分类讨论、进而得出结论.
解答:解:(1)当这两个都为负数时,
则:|x-5|+|x+t|=2,变为:-x+5-x-t=2,
可得:t=-2x+3,这时x为变量,则t也为变量,与题意不符;
(2)当这两个都为正数时,
则:|x-5|+|x+t|=2,变为:x-5+x-t=2,
可得:t=2x-7,这时x为变量,则t也为变量,与题意不符;
(3)当|x-5|为正数、|x+t|负数时,
则:|x-5|+|x+t|=2,变为:x-5-x-t=2,
可得:t=-7,这时x为变量,则t为定值,符合题意;
(4)当|x-5|为负数、|x+t|正数时,
则:|x-5|+|x+t|=2,变为:-x+5+x+t=2,
可得:t=-3,这时x为变量,则t为定值,符合题意;
故答案为:-3或-7.
点评:此题主要考查了绝对值的性质,解答此题应结合题意,分类讨论、进而得出结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在△ABC中,∠B与∠C的平分线交于点O,设∠A=x,∠BOC=y,当∠A变化时,写出y与x之间的函数关系式是
在△ABC中,∠B与∠C的平分线交于点O,设∠A=x,∠BOC=y,当∠A变化时,写出y与x之间的函数关系式是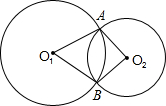 如图,⊙O1与⊙O2相交于点A、B,顺次连接O1、A、O2、B四点,得四边形O1AO2B.
如图,⊙O1与⊙O2相交于点A、B,顺次连接O1、A、O2、B四点,得四边形O1AO2B.