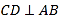Question

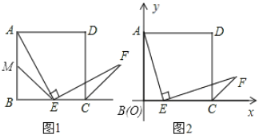
【题目】如图，矩形的顶点、分别在轴和轴上，点的坐标为，双曲线，的图象经过上的点与交于点，连接，若若是的中点﹒

(1)求点的坐标；

(2)点是边上一点，若和相似，求的解析式；

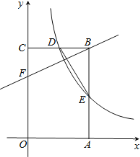
(3)若点也在此反比例函数的图象上（其中），过点作轴的垂线，交轴于点，若线段上存在一点，使得的面积是，设点的纵坐标为，求的值．

Answer 1

【答案】(1)点的坐标为；(2)的解析式为：，或；(3)．

【解析】

（1）先求出点E的坐标，求出双曲线的解析式，再求出CD＝1，即可得出点D的坐标；

（2）分两种情况：①△FBC和△DEB相似，当BD和BC是对应边时，，求出CF，得出F的坐标，用待定系数法即可求出直线BF的解析式；

②当BD与CF是对应边时，，求出CF、OF，得出F的坐标，用待定系数法即可求出直线BF的解析式；

（3）由题意得出m（3m+6 ）＝3，即m2+2m﹣1＝0，由三角形的面积得出mn＝1，代入得出n2﹣2n＝1，即可得出所求式子的值．

（1）∵四边形ABCD是矩形，∴OA＝BC，AB＝OC．

∵B（2，3），E为AB的中点，∴AB＝OC＝3，OA＝BC＝2，AE＝BEAB，∴E（2，），∴k＝23，∴双曲线解析式为：y；

∵点D在双曲线y（x＞0）上，∴OCCD＝3，∴CD＝1，∴点D的坐标为：（1，3）；

（2）∵BC＝2，CD＝1，∴BD＝1，分两种情况：

①△FBC和△DEB相似，当BD和BC是对应边时，，即，∴CF＝3，∴F（0，0），即F与O重合，设直线BF的解析式为：y＝kx，把点B（2，3）代入得：k，∴直线/span>BF的解析式为：yx；

②△FBC和△DEB相似，当BD与CF是对应边时，，即，∴CF，∴OF＝3，∴F（0，），设直线BF的解析式为：y＝ax+c，把B（2，3），F（0，）代入得：，解得：a，c，∴直线BF的解析式为：y；

综上所述：若△FBC和△DEB相似，BF的解析式为：yx或y；

（3）∵点P（m，3m+6）在反比例函数y的图象上，∴m（3m+6 ）＝3，整理得：m2+2m﹣1＝0．

∵PQ⊥x轴，∴Q点的坐标为：（m，n）．

∵△OQM的面积为，∴OMQM，∴OMQM＝1．

∵m＞0，∴mn＝1，∴m，代入m2+2m﹣1＝0得：1＝0，即n2﹣2n﹣1＝0，∴n2﹣2n＝1，∴n2﹣2n+9＝10．