Question

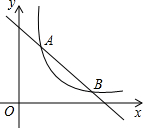
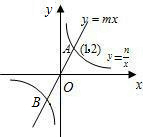
如图，Rt△ABC的顶点B在反比例函数y=

12

x

的图象上，AC边在x轴上，已知∠ACB=90°，∠A=30°，BC=4，则图中阴影部分的面积是（　　）

A．12

B．4 3

C．12-3 3

D．12- 3 2 3

Answer 1

∵∠ACB=90°，BC=4，
∴B点纵坐标为4，
∵点B在反比例函数y=

12

x

的图象上，
∴当y=4时，x=3，即B点坐标为（3，4），
∴OC=3．
在Rt△ABC中，∠ACB=90°，∠A=30°，BC=4，
∴AB=2BC=8，AC=

3

BC=4

3

，OA=AC-OC=4

3

-3．
设AB与y轴交于点D．
∵OD∥BC，
∴

OD

BC

=

OA

AC

，即

OD

4

=

4 3 -3

4 3

，
解得OD=4-

3

，
∴阴影部分的面积是：

1

2

（OD+BC）•OC=

1

2

（4-

3

+4）×3=12-

3

2

3

．
故选D．