题目内容
 (2006•厦门模拟)如图,一个正方体盒子的棱长为a厘米,顶点C′处有一 只昆虫甲,顶点A处有一只昆虫乙.假设昆虫甲在顶点C′处不动,昆虫乙沿盒壁爬行到昆虫甲的位置C′的最短路径的长是
(2006•厦门模拟)如图,一个正方体盒子的棱长为a厘米,顶点C′处有一 只昆虫甲,顶点A处有一只昆虫乙.假设昆虫甲在顶点C′处不动,昆虫乙沿盒壁爬行到昆虫甲的位置C′的最短路径的长是| 5 |
| 5 |
分析:首先根据题意画出平面展开图,可得CC′=AB=BC=a厘米,再在Rt△ACC′中利用勾股定理,即可算出AC′的长.
解答: 解:由题意画出平面展开图,如图所示:
解:由题意画出平面展开图,如图所示:
∵CC′=AB=BC=a厘米,
∴AC′=
=
=
a(厘米).
故答案为:
a.
 解:由题意画出平面展开图,如图所示:
解:由题意画出平面展开图,如图所示:∵CC′=AB=BC=a厘米,
∴AC′=
| AC2+CC′2 |
| (2a)2+a2 |
| 5 |
故答案为:
| 5 |
点评:此题主要考查了平面展开-最短路径问题,先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.

练习册系列答案
相关题目
 (2006•厦门模拟)如图,AB是斜靠在墙壁上的固定爬梯,梯脚B到墙脚C的距离1.6m,梯上一点D到墙面的距离1.4m,BD长0.5m,则梯子的长为( )
(2006•厦门模拟)如图,AB是斜靠在墙壁上的固定爬梯,梯脚B到墙脚C的距离1.6m,梯上一点D到墙面的距离1.4m,BD长0.5m,则梯子的长为( ) (2006•厦门模拟)下列几个函数图象可能如图所示的是函数( )
(2006•厦门模拟)下列几个函数图象可能如图所示的是函数( )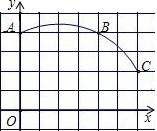 (2006•厦门模拟)如图,在平面直角坐标系中,一条圆弧经过正方形网格格点A,B,C,其中点B(4,4),则该圆弧所在圆的圆心坐标为
(2006•厦门模拟)如图,在平面直角坐标系中,一条圆弧经过正方形网格格点A,B,C,其中点B(4,4),则该圆弧所在圆的圆心坐标为