Question

在平面直角坐标系xOy中，已知直线y＝－x＋交x轴于点C，交y轴于点A．等腰直角三角板OBD的顶点D与点C重合，如图①所示．把三角板绕着点O顺时针旋转，旋转角度为α(0°＜α＜180°)，使B点恰好落在AC上的处，如图②所示．

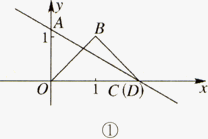
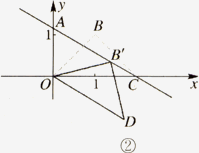
(1)求图①中的点B的坐标；

(2)求α的值；

(3)若二次函数y＝mx²＋3x的图象经过(1)中的点B，判断点是否在这条抛物线上，并说明理由．

Answer 1

答案：
解析：

解：(1)直线AC的解析式为，交轴于点C，交轴于点A， 　　点A的坐标为，点C的坐标为(2，0)………1分 　　等腰直角三角板OBD的顶点D与点C重合， 　　，∠BOD＝45° 　　过点B作于M 　　 　　 　　点B的坐标为(1，1)………2分 　　(2) 　　 　　过点O作于E．………3分 　　 　　 　　4分 　　(3)判断：点在这条抛物线上．………5分 　　理由：点在直线AC上， 　　设点的坐标为 　　 　　点的坐标为………6分 　　又二次函数过点B(1，1) 　　 　　二次函数的解析式为………7分 　　把代入，得 　　点在这条抛物线上．………8分 　　(注：对于每题的不同解法，请老师们根据评分标准酌情给分)