题目内容
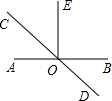如图所示，直线AB、CD相交O，OE⊥AB于O，且∠DOE=3∠COE，求∠AOD的度数．
解：∵∠DOE=3∠COE，∠DOE+∠COE=180°，
∴∠DOE=135°，
∵OE⊥AB，
∴∠BOD=45°，
∵∠AOB=180°，
∴∠AOD=∠AOB-∠BOD=135°．
分析：先根据∠DOE=3∠COE，和平角等于180°，可求出∠DOE，又OE⊥AB，故可得出∠DOB，再根据平角关系，即可得出∠AOD的度数．
点评：此题主要考查角的计算，注意垂直和平角的灵活运用．
∴∠DOE=135°，
∵OE⊥AB，
∴∠BOD=45°，
∵∠AOB=180°，
∴∠AOD=∠AOB-∠BOD=135°．
分析：先根据∠DOE=3∠COE，和平角等于180°，可求出∠DOE，又OE⊥AB，故可得出∠DOB，再根据平角关系，即可得出∠AOD的度数．
点评：此题主要考查角的计算，注意垂直和平角的灵活运用．
练习册系列答案
相关题目
12、如图所示，直线AB、CD相交于点O．若OM=ON=MN，那么∠APQ+∠CQP=
24、如图所示，直线AB与x轴交于A，与y轴交于B．
如图所示，直线AB与CD相交于点O，∠DOE=60°，∠BOE=27°，求∠BOD，∠AOD，∠AOC的度数．
如图所示，直线AB、CD相交于点O，∠BOD=40°，OA平分∠EOC，则∠EOD的度数为
如图所示，直线AB、CD、EF相交于点O，且EF⊥CD，若∠AOE=30°，则∠AOC=