题目内容
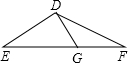 如图,已知△DEF中,DE=17cm,EF=30cm,EF边上的中线DG=8cm.求△DEF的面积.
如图,已知△DEF中,DE=17cm,EF=30cm,EF边上的中线DG=8cm.求△DEF的面积.
分析:由DE=17cm,EF=30cm,DG=8cm,可得△DEG为直角三角形,∠EDG=90°.要求△DEF的面积,需再求一高,可作DC⊥EF于C.设DC=xcm,CG=ycm,根据勾股定理,可求得x的值,即可求△DEF的面积.
解答: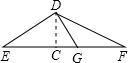 解:∵在△DEG中,DE=17cm,EG=
解:∵在△DEG中,DE=17cm,EG=
EF=15cm,DG=8cm.
∴EG2=DE2+DG2,△DEG为直角三角形,∠EDG=90°;
作DC⊥EF于C,设DC=xcm,CG=ycm,根据勾股定理,
在Rt△DCG中,x2+y2=82
在Rt△DCE中:x2+(15-y)2=172
解之得,x=8,y=0;
即DC与DG重合.
∴S△DEF=
×30×8=120cm2.
 解:∵在△DEG中,DE=17cm,EG=
解:∵在△DEG中,DE=17cm,EG=| 1 |
| 2 |
∴EG2=DE2+DG2,△DEG为直角三角形,∠EDG=90°;
作DC⊥EF于C,设DC=xcm,CG=ycm,根据勾股定理,
在Rt△DCG中,x2+y2=82
在Rt△DCE中:x2+(15-y)2=172
解之得,x=8,y=0;
即DC与DG重合.
∴S△DEF=
| 1 |
| 2 |
点评:本题综合考查了勾股定理及逆定理与二元二次方程,解这类题的关键是利用直角三角形,用勾股定理来寻求未知数的等量关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 20、如图,已知△DEF中,DE=17cm,EF=30cm,EF边上的中线DG=8cm.
20、如图,已知△DEF中,DE=17cm,EF=30cm,EF边上的中线DG=8cm. 如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论:
如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论: 如图,已知△DEF中,DE=17cm,EF=30cm,EF边上的中线DG=8cm.求△DEF的面积.
如图,已知△DEF中,DE=17cm,EF=30cm,EF边上的中线DG=8cm.求△DEF的面积.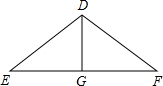 如图,已知△DEF中,DE=17cm,EF=30cm,EF边上的中线DG=8cm.
如图,已知△DEF中,DE=17cm,EF=30cm,EF边上的中线DG=8cm.