题目内容
如图，以△ABC的边AB、AC向外作等边△ABD和等边△ACE，连接CD、BE交于点P，则∠BPD的值是
- A.50°
- B.55°
- C.60°
- D.65°
C
分析：由等边三角形不难得出△DAC≌△BAE，即∠ACD=∠AEB，再利用角之间的转化，进而可得出结论．
解答：∵△ABD与△ACE是等边三角形，
∴AD=AB，AE=AC，∠BAD=∠CAE=60°，
∴∠DAB+∠BAC=∠CAE+∠BAC，
即∠DAC=∠BAE，
∴△DAC≌△BAE（SAS），
∴∠ACD=∠AEB，
∠DPE=∠BEC+∠ECP=∠BEC+∠ECA+∠ACD=120°，
∴∠BPD=60°．
故选C．
点评：本题主要考查了等边三角形的性质以及全等三角形的判定及性质，能够熟练运用其性质求解一些简单的计算问题．
分析：由等边三角形不难得出△DAC≌△BAE，即∠ACD=∠AEB，再利用角之间的转化，进而可得出结论．
解答：∵△ABD与△ACE是等边三角形，
∴AD=AB，AE=AC，∠BAD=∠CAE=60°，
∴∠DAB+∠BAC=∠CAE+∠BAC，
即∠DAC=∠BAE，
∴△DAC≌△BAE（SAS），
∴∠ACD=∠AEB，
∠DPE=∠BEC+∠ECP=∠BEC+∠ECA+∠ACD=120°，
∴∠BPD=60°．
故选C．
点评：本题主要考查了等边三角形的性质以及全等三角形的判定及性质，能够熟练运用其性质求解一些简单的计算问题．
练习册系列答案
相关题目
26、如图，以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE，四边形ADFE是平行四边形．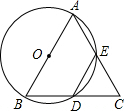
如图，以△ABC的边AB为直径作⊙O，交BC于D点，交AC于E点，BD=DE
（2011•峨眉山市二模）如图，以△ABC的边AB为直径作⊙O，BC与⊙O交于D，D是BC的中点，过D作DE⊥AC，交AC于点E．
（2010•黔东南州）如图，以△ABC的边BC为直径作⊙O分别交AB，AC于点F．点E，AD⊥BC于D，AD交于⊙O于M，交BE于H．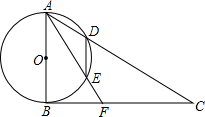
如图，以△ABC的边AB为直径的⊙O交AC于点D，弦DE∥AB，∠C=∠BAF