题目内容
已知:abc≠0,并且
=
=
=k,那么直线y=kx-k一定通过( )
| c |
| a+b |
| a |
| b+c |
| b |
| c+a |
| A、第一、二象限 |
| B、第二、三象限 |
| C、第一、三象限 |
| D、第一、四象限 |
分析:由于abc≠0,当a+b+c=0时,k=-1,由此即可确定直线y=kx-k通过的象限;当a+b+c≠0时,利用等比定理即可求出k=
,由此也可以确定直线y=kx-k通过的象限.
| 1 |
| 2 |
解答:解:∵abc≠0,
当a+b+c=0时,k=-1,
∴直线y=kx-k通过一、二、四第象限;
当a+b+c≠0时,
∵
=
=
=k,
∴
=k,
∴k=
,
∴直线y=kx-k通过一、三、四第象限,
∴直线y=kx-k一定通过一、四第象限.
故选D.
当a+b+c=0时,k=-1,
∴直线y=kx-k通过一、二、四第象限;
当a+b+c≠0时,
∵
| c |
| a+b |
| a |
| b+c |
| b |
| c+a |
∴
| a+b+c |
| 2(a+b+c) |
∴k=
| 1 |
| 2 |
∴直线y=kx-k通过一、三、四第象限,
∴直线y=kx-k一定通过一、四第象限.
故选D.
点评:本题考查了一次函数的图象的性质. 在直线y=kx+b中,当k>0时,经过第一三象限;当k<0时,经过二四象限.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图:已知:△ABC中,∠ABC、∠ACB的平分线,交于点O,过点O画EF∥BC交AB于点E,AC于点F.
如图:已知:△ABC中,∠ABC、∠ACB的平分线,交于点O,过点O画EF∥BC交AB于点E,AC于点F. 如图,已知在△ABC中,AB=AC,以AB为直径作⊙O交BC于F,连接OC交⊙O于D,连接BD并延长交AC于E,BC=
如图,已知在△ABC中,AB=AC,以AB为直径作⊙O交BC于F,连接OC交⊙O于D,连接BD并延长交AC于E,BC=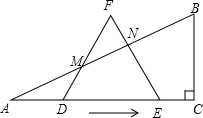 ),使边DF、EF与边AB分别相交于点M、N(M、N不与A、B重合).
),使边DF、EF与边AB分别相交于点M、N(M、N不与A、B重合). 如图,已知∠DAB+∠ABC+∠BCE=360°.
如图,已知∠DAB+∠ABC+∠BCE=360°.