题目内容
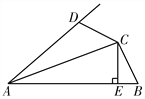
【题目】如图，在△ABC中，D是边AB上的动点，若在边AC，BC上分别有点E，F，使得
AE＝AD，BF＝BD．
(1)设∠C＝α，求∠EDF(用含α的代数式表示)；
(2)尺规作图：分别在边AB，AC上确定点P，Q(PQ不与DE平行或重合)，使得
∠CPQ＝∠EDF．(保留作图痕迹，不写作法)
【答案】（1）∠EDF＝90°－
α；（2）如图点P，Q即为所求见解析.
【解析】
（1）根据题中条件易知∠ADE＝（180°－∠A），∠BDF＝（180°－∠B）
再根据三角形内角和为180°，所以∠EDF＝90°－α
（2）作∠C的角平分线CP交AB于点P，过点P作AC的垂线，交AC于点Q.
（1）解：∵ AE＝AD，
∴ ∠AED＝∠ADE，
在△ADE中，
∠ADE＝（180°－∠A）．
同理可得∠BDF＝（180°－∠B）．
∴ ∠EDF＝180°－∠ADE－∠BDF
＝180°－（180°－∠A）－（180°－∠B）
＝（∠A＋∠B）．
在△ABC中，
∠A＋∠B＝180°－∠C＝180°－α．
∴ ∠EDF＝（180°－α）＝90°－α．
（2）解：尺规作图：如图点P，Q即为所求．
练习册系列答案
相关题目
【题目】设边长为
的正方形的中心
在直线
上，它的一组对边垂直于直线，半径为
的圆的圆心
在直线上运动，、两点之间的距离为
．
（
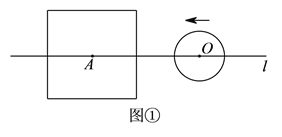
）如图①，当
时，填表：
| ⊙ |
|
|
|
|
| __________ |
| __________ |
| __________ |
（
）如图②，⊙与正方形有
个公共点
、
、
、
、
，求此时与
之间的数量关系：
（
）由（）可知，、、之间的数量关系和⊙与正方形的公共点个数密切相关．当
时，请根据、、
之间的数量关系，判断⊙与正方形的公共点个数．
（
）当与之间满足（）中的数量关系时，⊙与正方形的公共点个数为__________．
