题目内容
平面直角坐标系xOy中,抛物线![]() 与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.
与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.
(1) 求此抛物线的解析式;
(2) 若此抛物线的对称轴上的点P满足∠APB=∠ACB,求点P的坐标;
(3) Q为线段BD上一点,点A关于∠AQB的平分线的对称点为![]() ,若
,若![]() ,求点Q的坐标和此时△
,求点Q的坐标和此时△![]() 的面积.
的面积.
【解析】此题考核二次函数的的解析式的求解,以及运用图像与坐标轴的交点问题,能求解得到a,c关系式,然后把原解析式化简为关于a的表达式,![]() 然后借助于根的情况得到点B的坐标,从而得到与坐标轴y轴点C的坐标,得到a的值,得到求解。最后一问利用点A关于∠AQB的平分线的对称点为,对称性求解得到点的坐标,进而求解面积。
然后借助于根的情况得到点B的坐标,从而得到与坐标轴y轴点C的坐标,得到a的值,得到求解。最后一问利用点A关于∠AQB的平分线的对称点为,对称性求解得到点的坐标,进而求解面积。
解:(1)因为平面直角坐标系xOy中,抛物线![]() 与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.则点C(0,4a+c)A(1,0),令y=0,则得到
与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.则点C(0,4a+c)A(1,0),令y=0,则得到

抛物线的解析式为 .…………………… 3分
.…………………… 3分
(2)点![]() 的坐标为
的坐标为![]() .…………………………………………5分
.…………………………………………5分
由对称性得点 的坐标为
的坐标为![]() .……………………… 7分
.……………………… 7分
∴符合题意的点P的坐标为![]() 、
、![]() .
.
(3)点Q的坐标为![]() .…………………………………………… 10分
.…………………………………………… 10分
 此时
此时![]() .…12分
.…12分

练习册系列答案
相关题目
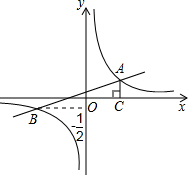 如图,已知在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,已知在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=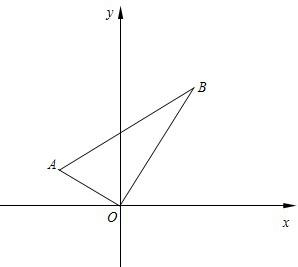 90°,∠A=60°,点A的坐标为(
90°,∠A=60°,点A的坐标为(
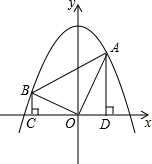 A,OB,OA⊥OB,作BC⊥x轴于C点,AD⊥x轴于D点.
A,OB,OA⊥OB,作BC⊥x轴于C点,AD⊥x轴于D点.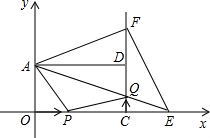 (2013•河东区一模)如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P、Q同时出发,同时停止,设运动时间为t秒,当t=2秒时
(2013•河东区一模)如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P、Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度,匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P、Q同时出发,同时停止,设运动时间为t秒,当t=2秒时