题目内容
17.如图,在四边形ABCD中,∠A=90°,AB=4cm,AD=2cm,BC=CD,E是AB上的一点.若沿CE折叠,则B,D两点重合,求△AED的面积.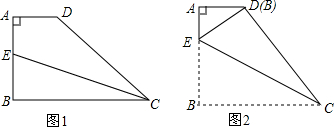
分析 设AE=x,由折叠的性质得到DE=BE=4-x,根据勾股定理列方程求得AE=$\frac{3}{2}$,于是得到△AED的面积=$\frac{1}{2}$AD•AE=$\frac{1}{2}×2×\frac{3}{2}$=$\frac{3}{2}$.
解答 解:设AE=x,由折叠的性质得:DE=BE=4-x,
∵∠A=90°,
∴AE2+AD2=DE2,
即x2+22=(4-x)2,
解得:x=$\frac{3}{2}$,
∴AE=$\frac{3}{2}$,
∴△AED的面积=$\frac{1}{2}$AD•AE=$\frac{1}{2}×2×\frac{3}{2}$=$\frac{3}{2}$.
点评 本题考查了折叠的性质,三角形的面积,勾股定理,熟练掌握折叠的性质是解题的关键.

练习册系列答案
相关题目
8.下列各式:5,2x-5=6,π,S=ab,2x-y,$\frac{5}{m+n}$,其中代数式的个数是( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
9.下列代数式中,值一定是正数的是( )
| A. | +m | B. | -m | C. | |m| | D. | |m|+1 |
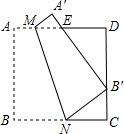 四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处.点A对应点为A′,且S△A′ME:S△CNB′=1:4,则AM的长是2.
四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处.点A对应点为A′,且S△A′ME:S△CNB′=1:4,则AM的长是2.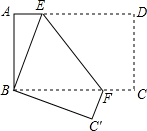 如图,长方形纸片ABCD,AD∥BC,将长方形纸片折叠,使点D与点B重合,点C落在点C′处,折痕为EF,
如图,长方形纸片ABCD,AD∥BC,将长方形纸片折叠,使点D与点B重合,点C落在点C′处,折痕为EF,