题目内容
等腰三角形一腰上的中线把其周长分成两部分的差为3cm，底边长为5cm，腰长为________．
8cm
分析：两部分之差可以是底边与腰之差，也可能是腰与底边之差，解答时应注意．设等腰三角形的腰长是xcm，根据其中一部分比另一部分长3cm，即可列方程求解．
解答：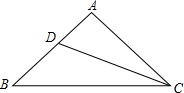
解：如图，设等腰三角形的腰长是xcm．
当AD+AC与BC+BD的差是3cm时，即
x+x-（x+5）=3
解得：x=8；
当BC+BD与AD+AC的差是3cm时，即5+x-（x+x）=3
解得：x=2（不符合三边关系，舍去）．
故腰长是8cm．
故答案为：8cm．
点评：本题主要考查了等腰三角形的计算，正确理解分两种情况讨论是解题的关键．
分析：两部分之差可以是底边与腰之差，也可能是腰与底边之差，解答时应注意．设等腰三角形的腰长是xcm，根据其中一部分比另一部分长3cm，即可列方程求解．
解答：
解：如图，设等腰三角形的腰长是xcm．当AD+AC与BC+BD的差是3cm时，即
x+x-（x+5）=3解得：x=8；
当BC+BD与AD+AC的差是3cm时，即5+
x-（x+x）=3解得：x=2（不符合三边关系，舍去）．
故腰长是8cm．
故答案为：8cm．
点评：本题主要考查了等腰三角形的计算，正确理解分两种情况讨论是解题的关键．
练习册系列答案
相关题目