题目内容
【题目】综合与探究
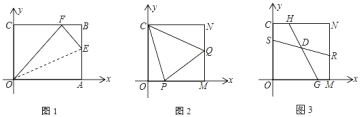
如图1,在平面直角坐标系中,点![]() 是坐标原点,点
是坐标原点,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的坐标为
的坐标为![]() ,四边形
,四边形![]() 是菱形,直线
是菱形,直线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.

(1)点![]() 的坐标是______;
的坐标是______;
(2)求直线![]() 的函数解析式;
的函数解析式;
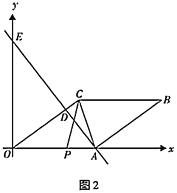
(3)如图2,动点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 方向以1个单位长度/秒的速度向终点
方向以1个单位长度/秒的速度向终点![]() 匀速运动,设
匀速运动,设![]() 的面积为
的面积为![]() (
(![]() ),点
),点![]() 的运动时间为
的运动时间为![]() 秒,求
秒,求![]() 与
与![]() 之间的函数关系式(要求写出自变量
之间的函数关系式(要求写出自变量![]() 的取值范围)
的取值范围)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
![]() 或
或![]()
![]() .
.
【解析】
(1)由点C坐标求OC的长,得到菱形边长为5,再根据CB∥x轴且CB=OC=5,即求出点B坐标;
(2)过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,由点C的坐标求出OF,CF的长,然后证得
轴,由点C的坐标求出OF,CF的长,然后证得![]() ,得出OD,AD的长,根据三角形的面积求出DH,再根据勾股定理求得OH,即可得点D坐标,然后利用待定系数法求得AD的解析式;
,得出OD,AD的长,根据三角形的面积求出DH,再根据勾股定理求得OH,即可得点D坐标,然后利用待定系数法求得AD的解析式;
(3)由点P在折线OAB上运动可知需分两种情况讨论.当点![]() 在
在![]() 边上运动时,根据
边上运动时,根据![]() 即可得出S与t的关系式;当点
即可得出S与t的关系式;当点![]() 在
在![]() 边上运动时,过点
边上运动时,过点![]() 作
作![]() ,可得
,可得![]() .根据
.根据![]() 即可得出S与t的关系式.
即可得出S与t的关系式.
解:(1)过点C作CF⊥x轴于点F,

∴∠CFO=90°
∵点C的坐标为(4,3),
∴OF=4,CF=3
∴OC=![]() =
=![]() =5,
=5,
∵四边形OABC是菱形,
∴OA=BC=OC=5,BC∥x轴,
∴yB=yC=3,xB=xC+5=9,
故答案为:(9,3);
(2)如答图1,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,

∵点![]() 的坐标为
的坐标为![]() ,∴
,∴![]() ,
,![]() .
.
∴![]() .
.
∵四边形![]() 为菱形,
为菱形,
∴![]() .
.
∴![]() .
.
在![]() 和
和![]() 中,
中,

∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∴ .
.
∴![]() .
.
设直线![]() 的函数解析式为
的函数解析式为![]() .
.
∵
解得
∴直线![]() 的函数解析式为
的函数解析式为![]() .
.
(3)分两种情况:
①当点![]() 在
在![]() 边上运动时,
边上运动时,
∴![]()
![]() .
.
②如答图2,当点![]() 在
在![]() 边上运动时,
边上运动时,
由(2)得![]() ,
,
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
∴![]() .
.
∴![]()
![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目