题目内容
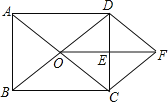
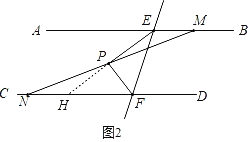
【题目】如图,AB∥CD,EF交AB于E,交CD于F,EP平分∠AEF,FP平分∠CFE,直线MN经过点P并与AB,CD分别交于点M,N.
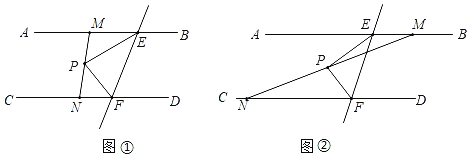
(1)如图①,求证:EM+FN=EF;
(2)如图②,(1)的结论是否成立?若成立,请证明;若不成立,直接写出EM,FN,EF三条线段的数量关系.
【答案】(1)证明见解析;(2)不成立,FN﹣EM=EF.
【解析】
(1)如图1(见解析),在EF上截取![]() ,易证
,易证![]() ,由三角形全等的性质得
,由三角形全等的性质得![]() ,由
,由![]() 得
得![]() ,再由邻补角定义可得
,再由邻补角定义可得![]() ,则
,则![]() ,从而可证
,从而可证![]() ,由三角形全等的性质得
,由三角形全等的性质得![]() ,则
,则![]() ;
;
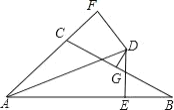
(2)如图2(见解析),延长EP交CD于H,由![]() 得
得![]() ,结合角平分线的定义得
,结合角平分线的定义得![]() ,则
,则![]() ,根据三角形全等的性质得
,根据三角形全等的性质得![]() ;又可证
;又可证![]() ,根据三角形全等的性质得
,根据三角形全等的性质得![]() ,故
,故![]() .
.
(1)如图1,在EF上截取![]()
![]() 平分
平分![]() ,
,![]() 平分
平分![]()
![]()
又![]()
![]()
![]()
由![]() 得
得![]() (两条直线平行,同旁内角互补)
(两条直线平行,同旁内角互补)
又![]() (邻补角)
(邻补角)
![]()
在![]() 和
和![]() 中,
中,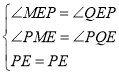
![]()
![]()
![]()
即![]() ;
;
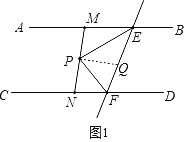
(2)题(1)的结论不成立
EM,FN,EF三条线段的数量关系是:![]() ,理由如下:
,理由如下:
如图2延长EP交CD于H
由![]() 得
得![]() (两条直线平行,同旁内角互补)
(两条直线平行,同旁内角互补)
![]() 平分
平分![]() ,
,![]() 平分
平分![]()
![]()
![]()
在![]() 和
和![]() 中,
中,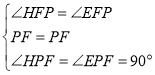
![]()
![]()
又![]()
![]() (两直线平行,内错角相等)
(两直线平行,内错角相等)
在![]() 和
和![]() 中,
中,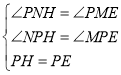
![]()
![]()
![]()
即![]() .
.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目