题目内容
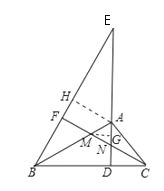
【题目】如图,已知![]() 为
为![]() 斜边BC上的高,点E为DA延长线上一点,连结
斜边BC上的高,点E为DA延长线上一点,连结![]() ,过点
,过点![]() 作
作![]() 于点F,交AB、AD于
于点F,交AB、AD于![]() 、
、![]() 两点.
两点.
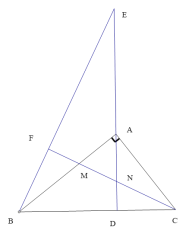
(1)证明:![]()
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
(3)若![]() ,且
,且![]() ,且线段BF与EF的长是关于
,且线段BF与EF的长是关于![]() 的一元二次方程
的一元二次方程![]() 的两个实数根,求
的两个实数根,求![]() 的长.
的长.
【答案】(1)见解析(2)DE=8.(3)BC=5.
【解析】
(1)判断出△BDE∽△NDC即可证明,
(2)先证明△ADC∽△BDA得到![]() ,即AD2=BDDC,再证明△EBD∽△CND,得到
,即AD2=BDDC,再证明△EBD∽△CND,得到![]() ,故BDDC=EDDN,AD2=EDDN,结合
,故BDDC=EDDN,AD2=EDDN,结合![]() ,
,![]() ,故AD=DN+AN=3,得到32=
,故AD=DN+AN=3,得到32=![]() DE,故可求解;
DE,故可求解;
(3)先证明∠ACM=∠FBM,由(2)可知∠E=∠FCB,∠ABE=∠E,AB=AE
过点M作MG⊥AN于点G,根据MG∥BD得![]() ,由
,由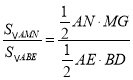 ,得到
,得到![]() ,故
,故![]() ,过点A作AH⊥EF于点H,再由AH∥FN,得
,过点A作AH⊥EF于点H,再由AH∥FN,得![]() ,设EH=8a,则FH=3a,得到BF=5a,EF=11a,由根与系数关系列出方程组解得:a=±
,设EH=8a,则FH=3a,得到BF=5a,EF=11a,由根与系数关系列出方程组解得:a=±![]() ,得到BF=
,得到BF=![]() ,再证明△ACN∽△BCM,得到
,再证明△ACN∽△BCM,得到![]() ,设AC=3b,则BC=5b,在Rt△ABC和 Rt△ACM中,求出MC=
,设AC=3b,则BC=5b,在Rt△ABC和 Rt△ACM中,求出MC=![]() b,再根据△ACM∽△FCB得
b,再根据△ACM∽△FCB得![]() ,得到
,得到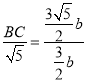 ,即可求解BC.
,即可求解BC.
(1)证明: ∵CF⊥BE,AD⊥CD,
∴∠EFN=∠NDC=90°,
又∠ENF=∠CND,
∴∠E=∠DCN,
又∠EDB=∠EDC=90°,
∴△BDE∽△NDC
∴![]()
故![]()
(2)解:∵∠BAC=90°,AD⊥BC,
∴∠ADC=∠ADB=90°,
∠DAC=∠DBA,
∴△ADC∽△BDA,
∴![]() ,
,
∴AD2=BDDC,
∵CF⊥BE,
∴∠FCB+∠EBD=90°,
∵∠E+∠EBD=90°,
∴∠E=∠FCB,
∵∠NDC=∠EDB=90°,
∴△EBD∽△CND,
∴![]() ,
,
∴BDDC=EDDN,
∴AD2=EDDN,
∵![]() ,
,![]() ,
,
∴AD=DN+AN=3,
∴32=![]() DE,
DE,
∴DE=8.
(3)∵AM=AN,
∴∠AMN=∠ANM
∵∠AMN+∠ACN=90°,∠DNC+∠NCD=90°,
∴∠ACM=∠NCD
∵∠BMF+∠FBM=90°,∠AMC+∠ACM=90°,
∴∠ACM=∠FBM
由(2)可知∠E=∠FCB,
∴∠ABE=∠E,
∴AB=AE
过点M作MG⊥AN于点G
由MG∥BD得![]() ,
,
∴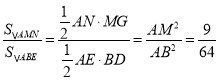 ,
,
∴![]() ,
,
∴![]() ,
,
过点A作AH⊥EF于点H,
由AH∥FN,
得![]() ,
,
设EH=8a,则FH=3a,
∵AE=AB,
∴BH=HE=8a,
∴BF=5a,EF=11a,
由根与系数关系得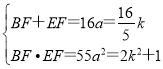 ,
,
解得:a=±![]() ,
,
∵a>0,a=![]() ,
,
∴BF=![]() ,
,
由∠ACM=∠MCB,∠DAC=∠DBA可知△ACN∽△BCM,
∴![]()
设AC=3b,则BC=5b
在Rt△ABC中,有AB=4b.
∴AM=![]() b.
b.
在Rt△ACM中,有MC=![]() b
b
由△ACM∽△FCB得![]() ,∴
,∴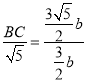 ,
,
∴BC=5.