Question

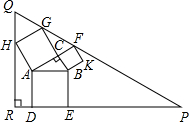如图，在Rt△ABC中，∠ACB=90°，∠BAC=30°，AB=4以Rt△ABC的三边向外作正方形ADEB、ACGH、CBKF，可得一“勾股图”．再作△PQR，使得∠R=90°，点H在边QR上，点D、E在边PR上，点G、F在边PQ上，那么△PQR的周长等于________．

Answer 1

27+13
分析：在直角△ABC中，根据三角函数即可求得AC，进而由等边三角形的性质和正方形的性质及三角函数就可求得QR的长，在直角△QRP中运用三角函数即可得到RP、QP的长，就可求出△PQR的周长．
解答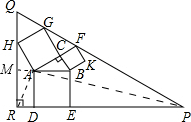：解：延长BA交QR于点M，连接AR，AP．
∵AC=GC，BC=FC，∠ACB=∠GCF，
∴△ABC≌△GFC，
∴∠CGF=∠BAC=30°，
∴∠HGQ=60°，
∵∠HAC=∠BAD=90°，
∴∠BAC+∠DAH=180°，
又∵AD∥QR，
∴∠RHA+∠DAH=180°，
∴∠RHA=∠BAC=30°，
∴∠QHG=60°，
∴∠Q=∠QHG=∠QGH=60°，
∴△QHG是等边三角形．
AC=AB•cos30°=4×=2，
则QH=HA=HG=AC=2，
在直角△HMA中，HM=AH•sin60°=2×=3，AM=HA•cos60°=，
在直角△AMR中，MR=AD=AB=4．
∴QR=2+3+4=7+2，
∴QP=2QR=14+4，
PR=QR•=6+7，
∴△PQR的周长等于RP+QP+QR=27+13，
故答案为：27+13．
点评：考查了勾股定理和含30度角的直角三角形，正确运用三角函数以及勾股定理是解决本题的关键．