题目内容
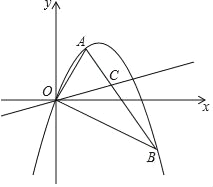
【题目】如图,抛物线y=ax2+bx经过△OAB的三个顶点,其中点A(1,![]() ),点B(3,﹣
),点B(3,﹣![]() ),O为坐标原点.
),O为坐标原点.
(1)求这条抛物线所对应的函数表达式;
(2)若P(4,m),Q(t,n)为该抛物线上的两点,且n<m,求t的取值范围;
(3)若C为线段AB上的一个动点,当点A,点B到直线OC的距离之和最大时,求∠BOC的大小及点C的坐标.
【答案】(1)![]() ;(2)t>4;(3)∠BOC=60°,C(
;(2)t>4;(3)∠BOC=60°,C(![]() ,
,![]() )
)
【解析】
(1)将已知点坐标代入y=ax2+bx,求出a、b的值即可;
(2)利用抛物线增减性可解问题;
(3)观察图形,点A,点B到直线OC的距离之和小于等于AB;同时用点A(1,![]() ),点B(3,﹣
),点B(3,﹣![]() )求出相关角度.
)求出相关角度.
(1)把点A(1,![]() ),点B(3,﹣
),点B(3,﹣![]() )分别代入y=ax2+bx得
)分别代入y=ax2+bx得
![]() ,解得
,解得
∴y=﹣![]()
(2)由(1)抛物线开口向下,对称轴为直线x=![]() ,
,
当x>![]() 时,y随x的增大而减小,
时,y随x的增大而减小,
∴当t>4时,n<m.
(3)如图,设抛物线交x轴于点F,分别过点A、B作AD⊥OC于点D,BE⊥OC于点E

∵AC≥AD,BC≥BE,
∴AD+BE≤AC+BE=AB,
∴当OC⊥AB时,点A,点B到直线OC的距离之和最大.
∵A(1,![]() ),点B(3,﹣
),点B(3,﹣![]() ),
),
∴∠AOF=60°,∠BOF=30°,
∴∠AOB=90°,
∴∠ABO=30°.
当OC⊥AB时,∠BOC=60°,点C坐标为(![]() ,
,![]() ).
).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校为了了解学生对语文、数学、英语、物理四科的喜爱程度(每人只选一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图:
科目 | 频数 | 频率 |
语文 |
| 0.5 |
数学 | 12 |
|
英语 | 6 |
|
物理 |
| 0.2 |
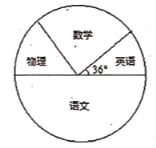
(1)求出这次调查的总人数;
(2)求出表中![]() 的值;
的值;
(3)若该校八年级有学生1000人,请你算出喜爱英语的人数,并发表你的看法.