题目内容
设正整数x≠y,且满足| 1 |
| x |
| 1 |
| y |
| 2 |
| 5 |
分析:先把原方程可化为:2xy-5x-5y=0,再变形为(2x-5)(2y-5)=25,因为正整数x≠y,所以25只能分解为25×1,得到2x-5=25,2y-5=1或2x-5=1,2y-5=25,即可解得x,y的值,从而计算出x2+y2的值.
解答:解:原方程可化为:2xy-5x-5y=0,
∴(2x-5)(2y-5)=25,
∵正整数x≠y,
∴2x-5=25,2y-5=1或2x-5=1,2y-5=25,
∴x=15,y=3或x=3,y=15,
∴x2+y2=32+152=234.
故答案为:234.
∴(2x-5)(2y-5)=25,
∵正整数x≠y,
∴2x-5=25,2y-5=1或2x-5=1,2y-5=25,
∴x=15,y=3或x=3,y=15,
∴x2+y2=32+152=234.
故答案为:234.
点评:本题考查了求二元二次方程的特殊解的方法.也考查了代数式的变形能力以及正整数解性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
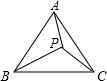 如图,P为等边△ABC内一点,PA、PB、PC的长为正整数,且PA2+PB2=PC2,设PA=m,n为大于5的实数,满m2n+30m+9n≤5m2+6mn+45,求△ABC的面积.
如图,P为等边△ABC内一点,PA、PB、PC的长为正整数,且PA2+PB2=PC2,设PA=m,n为大于5的实数,满m2n+30m+9n≤5m2+6mn+45,求△ABC的面积. 如图,P为等边△ABC内一点,PA、PB、PC的长为正整数,且PA2+PB2=PC2,设PA=m,n为大于5的实数,满m2n+30m+9n≤5m2+6mn+45,求△ABC的面积.
如图,P为等边△ABC内一点,PA、PB、PC的长为正整数,且PA2+PB2=PC2,设PA=m,n为大于5的实数,满m2n+30m+9n≤5m2+6mn+45,求△ABC的面积.