题目内容
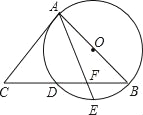
【题目】如图，AB，BC是⊙O的弦，∠B=60°，点O在∠B内，点D为
上的动点，点M，N，P分别是AD，DC，CB的中点．若⊙O的半径为2，则PN+MN的长度的最大值是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
连接OC、OA、BD，作OH⊥AC于H．首先求出AC的长，利用三角形的中位线定理即可解决问题.
解：连接OC、OA、BD，作OH⊥AC于H．
∵∠AOC＝2∠ABC＝120°，
∵OA＝OC，OH⊥AC，
∴∠COH＝∠AOH＝60°，CH＝AH，
∴CH＝AH＝OCsin60°＝
，
∴AC＝
，
∵CN＝DN，DM＝AM，
∴MN＝
，
∵CP＝PB，AN＝DN，
∴PN＝
，
当BD是直径时，PN的值最大，最大值为2，
∴PM＋MN的最大值为
．
故答案选：D．
练习册系列答案
阅读快车系列答案
相关题目
