题目内容
【题目】如图1,![]() ,
,![]() ,
,![]() ,
,![]() 分别是四边形
分别是四边形![]() 各边的中点,且
各边的中点,且![]() ,
,![]() ,
,![]() .
.

(1)试判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
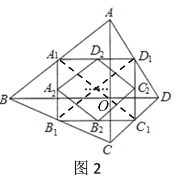
(2)如图2,依次取![]() ,
,![]() ,
,![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,
,![]() ,
,![]() ,再依次取
,再依次取![]() ,
,![]() ,
,![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,
,![]() ,
,![]() ……以此类推,取
……以此类推,取![]() ,
,![]() ,
,![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,
,![]() ,
,![]() ,根据信息填空:
,根据信息填空:
①四边形![]() 的面积是__________;
的面积是__________;
②若四边形![]() 的面积为
的面积为![]() ,则
,则![]() ________;
________;
③试用![]() 表示四边形
表示四边形![]() 的面积___________.
的面积___________.
【答案】(1)矩形,见解析;(2)①15,②5,③![]()
【解析】
(1)根据中位线定理,得出四边形![]() 是平行四边形,再根据
是平行四边形,再根据![]() 可判断四边形
可判断四边形![]() 为矩形;
为矩形;
(2)①根据题意算出A1B1=3,A1D1=5,可得四边形![]() 的面积;
的面积;
②根据题意算出A2D2= B2C2= C2D2=B2A2=![]() ,可得四边形
,可得四边形![]() 为菱形,得出四边形
为菱形,得出四边形![]() 的面积,以此类推得出
的面积,以此类推得出![]() =
=![]() ,令
,令![]() =
=![]() ,解出n即可;
,解出n即可;
③由②可得结果;
解:(1)四边形![]() 是矩形,
是矩形,
证明:∵![]() ,
,![]() ,
,![]() ,
,![]() 分别是四边形
分别是四边形![]() 各边的中点,
各边的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
同理可得![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
又∵![]() ,
,
易得![]() ,
,
∴四边形![]() 是矩形;
是矩形;
(2)①由题意可知:A1B1=![]() AC=3,A1D1=
AC=3,A1D1=![]() BD=5,
BD=5,
四边形![]() 的面积=3×5=15;
的面积=3×5=15;
②由构图过程可得:A2D2=B2C2=![]() B1D1=
B1D1=![]()
![]() =
=![]() ,C2D2=B2A2=
,C2D2=B2A2=![]() A1C1=
A1C1=![]()
![]() =
=![]() ,
,
可知四边形![]() 为菱形,
为菱形,
∴![]() =
=![]() =
=![]() =
=![]() ;
;
同理可求:![]() =
=![]() ,
,![]() =
=![]() ,…,
,…,![]() =
=![]() ,
,
故当四边形![]() 的面积为
的面积为![]() 时,
时,![]() =
=![]() ,
,
解得:n=5;
③由②可知:用![]() 表示四边形
表示四边形![]() 的面积为
的面积为![]() .
.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目