��Ŀ����
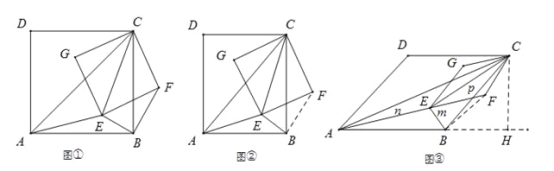
����Ŀ������С������10�֣���֪AC��EC�ֱ�Ϊ�ı���ABCD��EFCG�ĶԽ��ߣ���E����ABC�ڣ���CAE+��CBE=90��
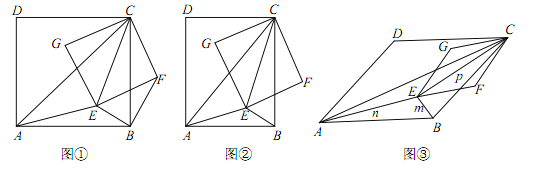
��1����ͼ�������ı���ABCD��EFCG��Ϊ������ʱ������BF��
i����֤����CAE�ס�CBF��
ii����BE=1��AE=2����CE�ij���
��2����ͼ�������ı���ABCD��EFCG��Ϊ���Σ���![]() ʱ����BE��1��AE=2��CE=3����k��ֵ��
ʱ����BE��1��AE=2��CE=3����k��ֵ��
��3����ͼ�������ı���ABCD��EFCG��Ϊ���Σ�����DAB=��GEF=45��ʱ����BE=m��AE=n��CE=p����̽��m��n��p����֮������ĵ�����ϵ����ֱ��д�����������д�������̣�
���𰸡���1��i��֤�������������ii��![]() ����2��
����2��![]() ����3��
����3��![]() ��
��
��������
���⣨1��i������ACE+��ECB=45������ BCF+��ECB=45�����õ���ACE=��BCF��������![]() ������CAE�ס�CBF��
������CAE�ס�CBF��
ii����![]() ���õ�BF=
���õ�BF=![]() ��������CAE�ס�CBF���õ���CAE=��CBF����һ���ɵõ���EBF=90�����Ӷ���
��������CAE�ס�CBF���õ���CAE=��CBF����һ���ɵõ���EBF=90�����Ӷ���![]() �����
�����![]() ��
��
��2������BF��ͬ���ɵã���EBF=90������![]() ���õ�
���õ�![]() ��
��![]() ����
����![]() ���Ӷ�
���Ӷ�![]() ���õ�
���õ�![]() ������ⷽ�̼��ɣ�
������ⷽ�̼��ɣ�
��3������BF��ͬ���ɵã���EBF=90������C��CH��AB�ӳ�����H���ɵã�
![]() ��
��![]() ��
��
��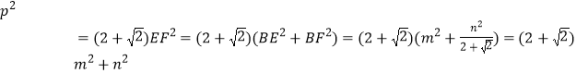 ��
��
�Ӷ���![]() ��
��
�����������1��i���ߡ�ACE+��ECB=45������ BCF+��ECB=45�������ACE=��BCF������![]() �����CAE�ס�CBF��
�����CAE�ס�CBF��
ii����![]() ����BF=
����BF=![]() ���ߡ�CAE�ס�CBF�����CAE=��CBF�����ߡ�CAE+��CBE=90�������CBF+��CBE=90��������EBF=90������
���ߡ�CAE�ס�CBF�����CAE=��CBF�����ߡ�CAE+��CBE=90�������CBF+��CBE=90��������EBF=90������![]() �����
�����![]() ��
��
��2������BF��ͬ���ɵã���EBF=90������![]() ����
����![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() ����
����![]() ����
����![]() �����
�����![]() ��
��
��3������BF��ͬ���ɵã���EBF=90������C��CH��AB�ӳ�����H���ɵã�
![]() ��
��![]() ��
��
��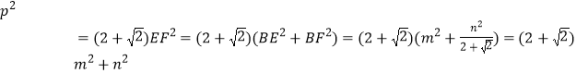 ��
��
��![]() ��
��