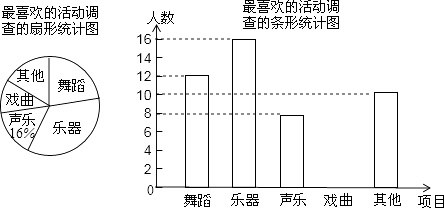
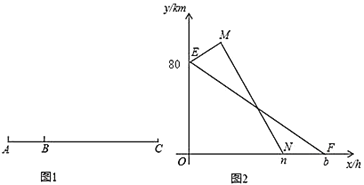
��Ŀ����
����Ŀ����ͼ��A��B��C����������һ����ֱ�Ĺ�·�ϣ�A��B�������40km��һ���׳���40km/h���ٶȴ�B�ص�C�أ�ͬʱһ���ҳ���80km/h���ٶȴ�B�ؿ���A�أ�����A�غ�Ȼ����120km/h���ٶȿ���C�أ������ڸ����ھ�������ʻ��ͼ���߶�EF������EMN�ֱ��ʾ�ס���������C�ص�·��y(ǧ��)����ʻʱ��x(Сʱ)֮��ĺ�����ϵͼ��
(1)д����M������Ϊ_______����E���������������________.
(2)��ֱ��д��n��b��ֵ��������߶�EF��MN�ĺ�����ϵʽ��
(3)����������Сʱ���ҳ��ϼ׳���
���𰸡�(1)(![]() ��120)��B�㵽C��ľ�����80km��(2)n=
��120)��B�㵽C��ľ�����80km��(2)n=![]() ��b=2���߶�EF�ĺ�����ϵʽ��
��b=2���߶�EF�ĺ�����ϵʽ��![]() ���߶�MN�ĺ�����ϵʽ��
���߶�MN�ĺ�����ϵʽ��![]() ��(3)
��(3)![]() Сʱ.
Сʱ.
��������
��1��������ҳ���B�ؿ���A������ʱ�䣬���ɵõ�M�����ꣻ�������֪��E���������������B�㵽C��ľ�����80km����2��nΪ�ҳ���B�ؿ���A���ٿ���C������ʱ�䣬bΪ�׳���B�ص�C�ص�ʱ�䣬�ʿɽ�����⣬�ó�M,N,F�����꣬���ɸ��ݴ���ϵ����ȷ��������ϵʽ����3������������ȣ������������������.
��1���ҳ���B�ؿ���A������ʱ��Ϊ![]() h������C��120km,
h������C��120km,
��M��![]() ��120����
��120����
��E���������������B�㵽C��ľ�����80km��
��2��nΪ�ҳ���B�ؿ���A���ٿ���C������ʱ�䣬��n=![]() +
+![]() =
=![]() ����N(
����N(![]() ,0)
,0)
bΪ�׳���B�ص�C�ص�ʱ��,��b=![]() ����F��2,0��
����F��2,0��
���߶�EFΪy=k1x+b1,����E��0,80����F(2��0)����߶�EF�ĺ�����ϵʽ��![]() ��
��
���߶�MNΪy=k2x+b2,����M��![]() ��120����N(
��120����N(![]() ,0)����߶�EF�ĺ�����ϵʽ��
,0)����߶�EF�ĺ�����ϵʽ��![]() ,
,
��3����![]() =
=![]()
���x=![]()
����������![]() Сʱ���ҳ��ϼ׳�.
Сʱ���ҳ��ϼ׳�.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�