题目内容
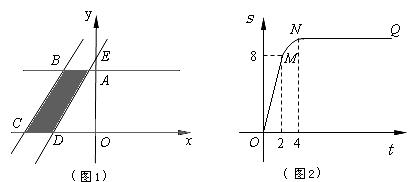
如图1所示,直角梯形OABC的顶点A、C分别在y轴正半轴与![]() 轴负半轴上.过点B、C作直线
轴负半轴上.过点B、C作直线![]() .将直线
.将直线![]() 平移,平移后的直线
平移,平移后的直线![]() 与
与![]() 轴交于点D,与
轴交于点D,与![]() 轴交于点E.
轴交于点E.
(1)将直线![]() 向右平移,设平移距离CD为
向右平移,设平移距离CD为![]() (t
(t![]() 0),直角梯形OABC被直线
0),直角梯形OABC被直线![]() 扫过的面积(图中阴影部份)为
扫过的面积(图中阴影部份)为![]() ,
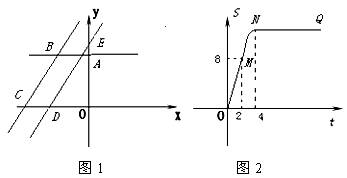
,![]() 关于
关于![]() 的函数图象如图2所示, OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
的函数图象如图2所示, OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
①求梯形上底AB的长及直角梯形OABC的面积;
②当![]() 时,求S关于
时,求S关于![]() 的函数解析式;
的函数解析式;
(2)在第(1)题的条件下,当直线![]() 向左或向右平移时(包括
向左或向右平移时(包括![]() 与直线BC重合),在直线AB上是否存在点P,使
与直线BC重合),在直线AB上是否存在点P,使![]() 为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
解:
(1)①![]()
![]() ,
,![]() ,S梯形OABC=12
,S梯形OABC=12
②当![]() 时,
时,
直角梯形OABC被直线![]() 扫过的面积=直角梯形OABC面积-直角三角开DOE面积
扫过的面积=直角梯形OABC面积-直角三角开DOE面积
![]()
(2) 存在
![]()
解法二:
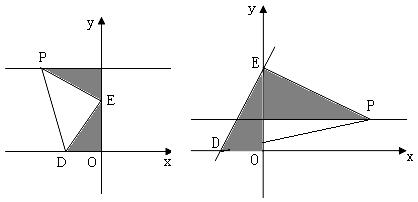
① 以点D为直角顶点,作![]() 轴
轴
![]()
![]() 设
设![]() .
.![]() (图示阴影)
(图示阴影)
![]()
![]()
![]() ,在上面二图中分别可得到
,在上面二图中分别可得到![]() 点的生标为P(-12,4)、P(-4,4)
点的生标为P(-12,4)、P(-4,4)
E点在0点与A点之间不可能;
② 以点E为直角顶点
同理在②二图中分别可得![]() 点的生标为P(-
点的生标为P(-![]() ,4)、P(8,4)E点在0点下方不可能.
,4)、P(8,4)E点在0点下方不可能.
③ 以点P为直角顶点
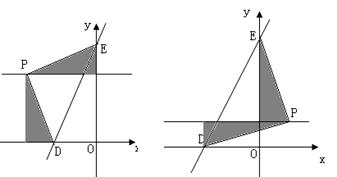
同理在③二图中分别可得![]() 点的生标为P(-4,4)(与①情形二重合舍去)、P(4,4),
点的生标为P(-4,4)(与①情形二重合舍去)、P(4,4),
E点在A点下方不可能.
综上可得![]() 点的坐标共5个解,分别为P(-12,4)、P(-4,4)、P(-
点的坐标共5个解,分别为P(-12,4)、P(-4,4)、P(-![]() ,4)、
,4)、
P(8,4)、P(4,4).
下面提供参考解法三:
以直角进行分类进行讨论(分三类):
第一类如上解法⑴中所示图![]()
![]()
![]()
![]() ,直线
,直线![]() 的中垂线方程:
的中垂线方程:![]() ,令
,令![]() 得
得![]() .由已知可得
.由已知可得![]() 即
即![]() 化简得
化简得![]() 解得
解得 ![]()
![]() ;
;
第二类如上解法②中所示图![]()
![]() ,
,
直线![]() 的方程:
的方程:![]() ,令
,令![]() 得
得![]() .
.
由已知可得![]() 即
即![]() 化简得
化简得![]() 解之得 ,
解之得 ,![]()
![]()
第三类如上解法③中所示图![]()
![]()
,直线![]() 的方程:
的方程:![]() ,令
,令![]() 得
得![]() .由已知可得
.由已知可得![]() 即
即![]() 解得
解得![]()
![]() (
(![]() 与
与![]() 重合舍去).
重合舍去).
综上可得![]() 点的坐标共5个解,分别为P(-12,4)、P(-4,4)、P(-
点的坐标共5个解,分别为P(-12,4)、P(-4,4)、P(-![]() ,4)、
,4)、
P(8,4)、P(4,4).
事实上,我们可以得到更一般的结论:
如果得出![]()
![]() 设
设![]() ,则P点的情形如下
,则P点的情形如下
| 直角分类情形 |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
| ||
|
|
|
|
|
|
|





