题目内容
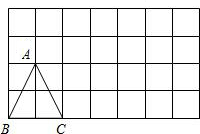
如图，方格纸中△A′B′C′的面积是△ABC的面积的________倍，线段A′B′是AB的________倍．
4 2
分析：设一个小方格的边长为1，利用勾股定理可以求出△ABC和△A′B′C′的各边的长，再看对应边的比是不是相等，相等则两个三角形相似．那么它们的对应边的比的平方等于面积比，可得出A′B′与AB的关系．
解答：根据勾股定理，可求出AB=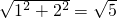
，
同理可求出A′B′=
，
B′C′=
，BC=
，
∴
=
，
∴△ABC∽△A′B′C′，
∴A′B′是AB的2倍．
点评：本题利用了勾股定理，以及相似三角形的判定（三边对应成比例的两个三角形相似）及性质．
分析：设一个小方格的边长为1，利用勾股定理可以求出△ABC和△A′B′C′的各边的长，再看对应边的比是不是相等，相等则两个三角形相似．那么它们的对应边的比的平方等于面积比，可得出A′B′与AB的关系．
解答：根据勾股定理，可求出AB=
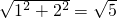，同理可求出A′B′=
，B′C′=
，BC=，∴
=，∴△ABC∽△A′B′C′，
∴A′B′是AB的2倍．
点评：本题利用了勾股定理，以及相似三角形的判定（三边对应成比例的两个三角形相似）及性质．
练习册系列答案
相关题目
C1绕点A1逆时针旋转180°，得到△A1B2C2．
20、如图，方格纸中有三个点A、B、C，按要求作出四边形，四边形的各顶点在格点上．
结合所给的平面直角坐标系解答下列问题：
如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，-2）．