Question

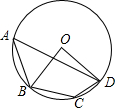
如图所示，圆O是△ABC的外接圆，∠BAC与∠ABC的平分线相交于点I，延长AI交圆O于点D，连接BD、DC．
（1）求证：BD=DC=DI；
（2）若圆O的半径为10cm，∠BAC=120°，求△BDC的面积．

Answer 1

（1）证明：∵AI平分∠BAC，
∴∠BAD=∠DAC，
∴

BD

=

DC

，
∴BD=DC．
∵BI平分∠ABC，
∴∠ABI=∠CBI．
∵∠BAD=∠DAC，∠DBC=∠DAC，
∴∠BAD=∠DBC．
又∵∠DBI=∠DBC+∠CBI，∠DIB=∠ABI+∠BAD，
∴∠DBI=∠DIB，
∴△BDI为等腰三角形，
∴BD=ID，
∴BD=DC=DI．

（2）当∠BAC=120°时，△ABC为钝角三角形，
∴圆心O在△ABC外．
连接OB、OD、OC．
∴∠DOC=∠BOD=2∠BAD=120°，
∴∠DBC=∠DCB=60°，
∴△BDC为正三角形．
∴OB是∠DBC的平分线，
延长CO交BD于点E，则OE⊥BD，
∴BE=

1

2

BD，
又∵OB=10，
∴BD=2OBcos30°=2×10×

3

2

=10

3

．
∴CE=BD•sin60°=10

3

×

3

2

=15，
∴S_△BDC=

1

2

BD•CE=

1

2

×10

3

×15=75

3

．
答：△BDC的面积为75

3

cm²．