题目内容
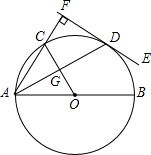（2013•曲靖）如图，⊙O的直径AB=10，C、D是圆上的两点，且 |
| AC |
|
| CD |
|
| DB |
（1）求证：DF⊥AF．
（2）求OG的长．
分析：（1）连接BD，根据
=
=
，可得∠CAD=∠DAB=30°，∠ABD=60°，从而可得∠AFD=90°；
（2）根据垂径定理可得OG垂直平分AD，继而可判断OG是△ABD的中位线，在Rt△ABD中求出BD，即可得出OG．
|
| AC |
|
| CD |
|
| DB |
（2）根据垂径定理可得OG垂直平分AD，继而可判断OG是△ABD的中位线，在Rt△ABD中求出BD，即可得出OG．
解答：
解：（1）连接BD，
∵
=
=
，
∴∠CAD=∠DAB=30°，∠ABD=60°，
∴∠ADF=∠ABD=60°，
∴∠CAD+∠ADF=90°，
∴DF⊥AF．
（2）在Rt△ABD中，∠BAD=30°，AB=10，
∴BD=5，
∵
=
，
∴OG垂直平分AD，
∴OG是△ABD的中位线，
∴OG=
BD=
．
解：（1）连接BD，∵
|
| AC |
|
| CD |
|
| DB |
∴∠CAD=∠DAB=30°，∠ABD=60°，
∴∠ADF=∠ABD=60°，
∴∠CAD+∠ADF=90°，
∴DF⊥AF．
（2）在Rt△ABD中，∠BAD=30°，AB=10，
∴BD=5，
∵
|
| AC |
|
| CD |
∴OG垂直平分AD，
∴OG是△ABD的中位线，
∴OG=
| 1 |
| 2 |
| 5 |
| 2 |
点评：本题考查了切线的性质、圆周角定理及垂径定理的知识，解答本题要求同学们熟练掌握各定理的内容及含30°角的直角三角形的性质．
练习册系列答案
相关题目
（2013•曲靖）如图是某几何体的三视图，则该几何体的侧面展开图是（ ）
（2013•曲靖）如图，在?ABCD中，对角线AC与BD相交于点O，过点O作EF⊥AC交BC于点E，交AD于点F，连接AE、CF．则四边形AECF是（ ）
（2013•曲靖）如图，以∠AOB的顶点O为圆心，适当长为半径画弧，交OA于点C，交OB于点D．再分别以点C、D为圆心，大于
（2013•曲靖）如图，直线AB、CD相交于点O，若∠BOD=40°，OA平分∠COE，则∠AOE=