Question

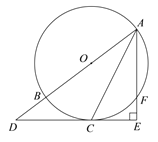
【题目】如图，BD为⊙O的直径，点A是劣弧BC的中点，AD交BC于点E，连结AB.

(1)求证：AB2=AE·AD；

(2)若AE=2，ED=4，求图中阴影的面积．

Answer 1

【答案】(1)见解析;(2) 2π-3.

【解析】

（1）点A是劣弧BC的中点，即可得∠ABC=∠ADB，又由∠BAD=∠EAB，即可证得△ABE∽△ADB，根据相似三角形的对应边成比例，即可证得AB2=AEAD.

(2) 连结OA，由S阴影=S扇形AOB-S△AOB求出即可.

(1)证明：∵点A是劣弧BC的中点，

∴=

∴∠ABC=∠ADB．

又∵∠BAD=∠EAB，∴△ABE∽△ADB．

∴ ．

∴AB2=AEAD．

(2)解：连结OA

∵AE=2，ED=4，

由(1)可知

∴AB2=AEAD，

∴AB2=AEAD=AE(AE+ED)=2×6=12．

∴AB=(舍负)．

∵BD为⊙O的直径，

∴∠BAD=90°．

在Rt△ABD中，BD=

∴OB=．

∴OA=OB=AB=

∴△AOB为等边三角形

∴∠AOB=60°．

S阴影=S扇形AOB-S△AOB=