题目内容
关于抛物线y=(x-1)2+2,下列结论中不正确是
- A.对称轴为直线x=1
- B.当x<1时,y随x的增大而减小
- C.与x轴没有交点
- D.与y轴交于点(0,2)
D
分析:由抛物线解析式得到顶点坐标,进而确定出对称轴为直线x=1,选项A正确;根据抛物线开口向上,得到x小于1时,抛物线为减函数,即y随x的增大而减小,得到选项B正确;再求出b2-4ac的值小于0,得到抛物线与x轴没有交点,选项C正确,令抛物线解析式中x=0,求出y=3,得到抛物线与y轴交点为(0,3),故选项D错误.
解答:抛物线y=(x-1)2+2,
∴顶点坐标为(1,2),对称轴为直线x=1,开口向上,
∴x<1时,y随x的增大而减小;当x>1时,y随x的增大而增大,
又y=(x-1)2+2=x2-2x+3,令x=0,求出y=3,
∴b2-4ac=4-12=-8<0,抛物线与y轴的交点为(0,3),
∴抛物线与x轴没有交点,
则选项中错误的是D.
故选D.
点评:此题考查了抛物线与x轴的交点,二次函数y=ax2+bx+c与x轴的交点由b2-4ac来决定,当b2-4ac<0,抛物线与x轴没有交点;当b2-4ac=0,抛物线与x轴只有一个交点;当b2-4ac>0时,抛物线与x轴有两个交点.
分析:由抛物线解析式得到顶点坐标,进而确定出对称轴为直线x=1,选项A正确;根据抛物线开口向上,得到x小于1时,抛物线为减函数,即y随x的增大而减小,得到选项B正确;再求出b2-4ac的值小于0,得到抛物线与x轴没有交点,选项C正确,令抛物线解析式中x=0,求出y=3,得到抛物线与y轴交点为(0,3),故选项D错误.
解答:抛物线y=(x-1)2+2,
∴顶点坐标为(1,2),对称轴为直线x=1,开口向上,
∴x<1时,y随x的增大而减小;当x>1时,y随x的增大而增大,
又y=(x-1)2+2=x2-2x+3,令x=0,求出y=3,
∴b2-4ac=4-12=-8<0,抛物线与y轴的交点为(0,3),
∴抛物线与x轴没有交点,
则选项中错误的是D.
故选D.
点评:此题考查了抛物线与x轴的交点,二次函数y=ax2+bx+c与x轴的交点由b2-4ac来决定,当b2-4ac<0,抛物线与x轴没有交点;当b2-4ac=0,抛物线与x轴只有一个交点;当b2-4ac>0时,抛物线与x轴有两个交点.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 7、如图,关于抛物线y=(x-1)2-2,下列说法错误的是( )
7、如图,关于抛物线y=(x-1)2-2,下列说法错误的是( )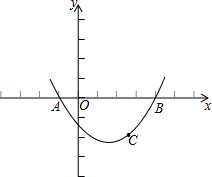 如图,已知抛物线过点A(-1,0)、B(4,0)、
如图,已知抛物线过点A(-1,0)、B(4,0)、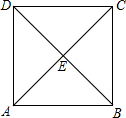 如图,已知正方形ABCD的边长为2,将此正方形置于直角坐标系xOy中,使AB在x轴上,对角线的交点E在直线y=x-1上.
如图,已知正方形ABCD的边长为2,将此正方形置于直角坐标系xOy中,使AB在x轴上,对角线的交点E在直线y=x-1上. (2012•温州)如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP.
(2012•温州)如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP.