题目内容
函数
的图象是抛物线，则m=________．
-1
分析：根据二次函数的定义列式求解即可．
解答：根据二次函数的定义，m2+1=2且m-1≠0，
解得m=±1且m≠1，
所以，m=-1．
故答案为：-1．
点评：本题考查二次函数的定义，要注意二次项的系数不等于0．
分析：根据二次函数的定义列式求解即可．
解答：根据二次函数的定义，m2+1=2且m-1≠0，
解得m=±1且m≠1，
所以，m=-1．
故答案为：-1．
点评：本题考查二次函数的定义，要注意二次项的系数不等于0．
练习册系列答案
相关题目
蔬菜基地种植某种蔬菜，由市场行情分析知，1月份至6月份这种蔬菜的上市时间x（月份）与市场售价p（元/千克）的关系如下表：
这种蔬菜每千克的种植成本y（元/千克）与上市时间x（月份）满足一个函数关系，这个函数的图象是抛物线的一段（如图）．
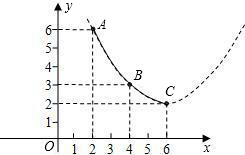
（1）写出上表中表示的市场售价p（元/千克）关于上市时间x（月份）的函数关系式 ；
（2）若图中抛物线过A，B，C点，写出抛物线对应的函数关系式 ；
（3）由以上信息分析， 月份上市出售这种蔬菜每千克的收益最大，最大值为 元（收益=市场售价一种植成本）．
| 上市时间x（月份） | 1 | 2 | 3 | 4 | 5 | 6 |
| 市场售价p（元/千克） | 10.5 | 9 | 7.5 | 6 | 4.5 | 3 |
（1）写出上表中表示的市场售价p（元/千克）关于上市时间x（月份）的函数关系式
（2）若图中抛物线过A，B，C点，写出抛物线对应的函数关系式
（3）由以上信息分析，
蔬菜基地种植某种蔬菜，由市场行情分析知，1月份至6月份这种蔬菜的上市时间x（月份）与市场售价p（元/千克）的关系如下表：
这种蔬菜每千克的种植成本y（元/千克）与上市时间x（月份）满足一个函数关系，这个函数的图象是抛物线的一段（如图）．
（1）写出上表中表示的市场售价p（元/千克）关于上市时间x（月份）的函数关系式；
（2）若图中抛物线过A，B，C点，写出抛物线对应的函数关系式；
（3）由以上信息分析，哪个月上市出售这种蔬菜每千克的收益最大？最大值为多少？（收益=市场售价-种植成本）
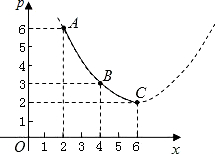
| 上市时间x（月份） | 1 | 2 | 3 | 4 | 5 | 6 |
| 市场销售p（元/千克） | 10.5 | 9 | 7.5 | 6 | 4.5 | 3 |
（1）写出上表中表示的市场售价p（元/千克）关于上市时间x（月份）的函数关系式；
（2）若图中抛物线过A，B，C点，写出抛物线对应的函数关系式；
（3）由以上信息分析，哪个月上市出售这种蔬菜每千克的收益最大？最大值为多少？（收益=市场售价-种植成本）
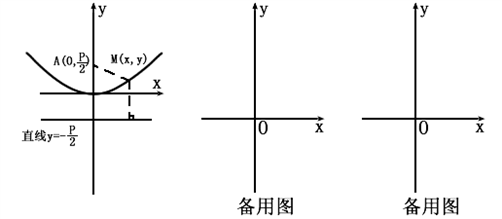
（2011•包河区一模）蔬菜基地种植某种蔬菜，由市场行情分析可知，1月份到6月份这种蔬菜的市场售价p（元/千克）与上市时间x（月份）的关系为p=-1.5x+12，这种蔬菜每千克的种植成本y（元/千克）与上市时间x（月份）满足一个函数关系，这个函数的图象是抛物线一部分，如图所示．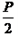
）的距离与它到定直线y= -
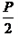的距离相等，那么动点M形成的图形就是抛物线
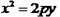(p>0)，如图。
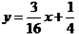相交于B、C两点，求△OBC的面积。