题目内容
 如图,AD为△ABC的中线,BE为三角形ABD中线,
如图,AD为△ABC的中线,BE为三角形ABD中线,(1)在△BED中作BD边上的高EF;
(2)若△ABC的面积为60,BD=5,求EF的长.
分析:(1)直接利用直角三角尺最值三角形的高;
(2)利用三角形中线的性质得出S△BDE=
S△ABC,进而借助三角形面积公式求出即可.
(2)利用三角形中线的性质得出S△BDE=
| 1 |
| 4 |
解答: 解;(1)如图所示;
解;(1)如图所示;
(2)∵AD为△ABC的中线,BE为三角形ABD中线,
∴S△ABD=
S△ABC,S△BDE=
S△ABD,
∴S△BDE=
S△ABC,
∵△ABC的面积为60,BD=5,
∴
×5×EF=15,
∴EF=6.
 解;(1)如图所示;
解;(1)如图所示;(2)∵AD为△ABC的中线,BE为三角形ABD中线,
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BDE=
| 1 |
| 4 |
∵△ABC的面积为60,BD=5,
∴
| 1 |
| 2 |
∴EF=6.
点评:此题主要考查了基本作图以及三角形中线的性质,根据三角形中线平分三角形面积得出是解题关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
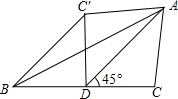 如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长.
如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长.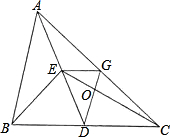 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线. 如图,AD为△ABC的中线,BE为三角形ABD中线,
如图,AD为△ABC的中线,BE为三角形ABD中线, 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线. 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.