题目内容
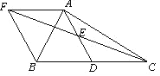
【题目】如图,⊙O为正方形ABCD的外接圆,E为弧BC上一点,AF⊥DE于F,连OF、OD.
(1)求证:AF=EF;
(2)若![]() ,求sin∠DOF的值.
,求sin∠DOF的值.
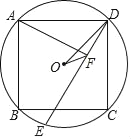
【答案】(1)见解析;(2)![]()
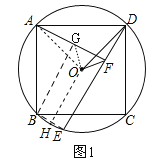
【解析】试题分析:(1)如图,过B作BG⊥AF于G,连接BE、OB,只要证明四边形BGEF是矩形,△ABG≌△DAF即可解决问题;
(2)作OH⊥BE于H,连接AO,GO.首先证明OH垂直平分线段FG,再证明∠DOF=∠DAF,△FOG是等腰直角三角形即可解决问题;
试题解析:证明:(1)如图,过B作BG⊥AF于G,连接BE、OB.∵AF⊥DE,∴∠AGB=∠AFD=90°,∴∠BAF+∠ABG=90°.∵四边形ABCD是正方形,∴BD为⊙O的直径,AD=AB,∠BAD=90°,∴∠DAF+∠BAF=90°,∠BED=90°,∴∠ABG=∠DAF,∴△ABG≌△DAF,∴BG=AF.∵∠BED=∠BGF=∠AFE=90°,∴四边形GBEF是矩形,∴EF=BG,∴AF=EF;
(2)作OH⊥BE于H,连接AO,GO.
∵OH⊥BE,∴BH=HE,∴OH垂直平分线段BE.∵四边形GBEF是矩形,∴BE=GF,BE∥GF,∴OH垂直平分线段FG,∴OG=OF.∵∠AOD=∠AFD=90°,∴A、D、F、O四点共圆,∴∠DOF=∠DAF,∠OFG=∠ADO=45°,∴△FOG是等腰直角三角形,∴FG=![]() OF.∵EF=BG=AF=2
OF.∵EF=BG=AF=2![]() OF,∴AF=2FG,AG=FG=DF,设DF=a,则AF=2a,AD=
OF,∴AF=2FG,AG=FG=DF,设DF=a,则AF=2a,AD=![]() a,∴sin∠DOF=sin∠DAF=
a,∴sin∠DOF=sin∠DAF=![]() =
=![]() .
.

练习册系列答案
相关题目